우리는 실생활에서 어떤 것을 최적화를 하고 싶어한다.
예를들어, 나에게 10분이 주어질 때, 제일 최적의 경로를 예측한다고 하면, 커피를 뽑고, 모니터를 키고, 모니터를 키는 동안 약을 먹고, 약을 먹는동안 다 내려진 커피를 가지고 정수기로 가서 물을 담는다.
이러한 과정을 어찌보면 실생활에서 누구나 쓰는 최적화 기법이다.
조금만 더 ML 관점으로 적어보자.
보통 Deep Learning은 아키텍쳐의 구조, 신경망의 깊이와 넓이, L1, L2 계수, batch 크기, epoch 크기 등등 정말 수십가지의 hyperparameter들이 존재한다. 이러한 parameter 들을 어떤 파라미터들을 어떻게 적용했을 때, 제일 최상의 max 하기 위해서는 어떻게 조절해야하는지 궁금하다.
이러한 과정도 최적화, Optimization이 적용된 기법이다.
cf) Search의 종류
search 종류는 manual, grid, random search가 있다. 실제로 기존 search는 불필요한 탐색이 많기 때문에 다른 optimization 기법들은 기존 search를 활용, 응용하여 쓴다.
이는 어느 optimization을 할 때, 모두 적용되며 자세한 내용은 아래의 링크를 통해서 보자.
2020/09/16 - [AI] - Ai : Search (Manual, Grid, Random)
Ai : Search (Manual, Grid, Random)
우리들의 모든 ai 모델들은 data 기반으로 Model이 train되고 test가 이루어진다. 또한 data 기반으로 만들어지는 Model들은 여러 Hyperparameter를 가지게 된다. 그래서 인간들은 인간이 정해주어야하는 Hyper
mambo-coding-note.tistory.com
Bayesian Optimization의 정의
Random Search와 통계적인 기법 (Gaussian Distribution)을 기반으로 실제 data를 이용하여 surrogate model을 이용하여 실제 model을 찾지 않아도 Maximum value를 도출해낼 수 있다.
cf) surrogate model
목적
Surrogate model(대체 모델, 근사수학모델)이란 자동차 충돌 실험과 같이 제한된 계산 비용이 많이 드는 시뮬레이션을 기반으로 복잡한 시스템의 수많은 입출력 특성을 실제 모형과 유사하게 만드는 것을 목적으로 하는 소형 확장 분석 모델을 일컫는 말입니다.
적용
Surrogate model은 시뮬레이션 모델의 복잡한 동작을 흉내낼 수 있으며, 이러한 특성은 설계 자동화, 매개변수 분석, 우주 탐사에 관한 설계, 최적화 및 민감도 분석등에 사용될 수 있습니다.
출처: https://elecs.tistory.com/344
Surrogate model(대체 모델)
Surrogate model(대체 모델, 근사수학모델)이란 자동차 충돌 실험과 같이 제한된 계산 비용이 많이 드는 시뮬레이션을 기반으로 복잡한 시스템의 수많은 입출력 특성을 실제 모형과 유사하게 만드�
elecs.tistory.com
Bayesian Optimization의 목적
1. (탐색 대상 함수의 해당 하이퍼파라미터, 탐색 대상 함수)를 쌍(pair)으로 만들어,
2. 이를 대상으로 Surrogate Model (임의의 모델)을 만들고 평가를 통해 순차적으로 업데이트, 최적의 하이퍼파라미터 조합을 탐색한다.
Acquisition Function (제일 중요)
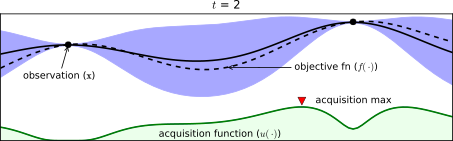
위의 그림을 보면 위의 보라색 그래프가 posterior graph이다. 즉 data 기반으로 model에 적용하였을 때 가지는 function을 그래프로 표현한 것이다. 그리고 초록색 그래프가 바로 acquisiton function이며, 실제로 Bayesian Optimization에서 decision 을 담당하는 부분이라 굉장히 중요하다.
- 목적
Acquisiton Function 은 surrogate model이 목적함수 (우리가 찾고자 하는 함수) 에 대하여 실제 데이터를 기반으로 다음 번 조사할 x 값을 확률적으로 계산하여 추천해주는 함수이다.
여기서 등장하는 개념이 Exploitation, Exploration 개념이다.
Exploitation 은 현재까지 조사된 값들의 근방으로 다시 조사를 하는 것이다. 착취를 말한다.
Exploration 은 현재까지 조사된 값들의 근방으로 조사를 하지 않고, 불확실성이 제일 높은 구간을 조사한다. 탐험을 말한다.
EI (Expected Improvement)는 Exploration 과 Exploitation 방법을 모두 일정 수준 포함하도록 설계된 것이고, 제일 많이 쓰는 Acquistion Function이다. 위는 Gaussian Process를 적용한 그래프다.
1. POI (Probability of Improvement)
cf ) scipy.stats.norm (확률분포 및 정규분포)
from scipy.stats import norm
# ppf : 누적분포함수의 역함수(inverse cumulative distribution function)
>>> a = norm.ppf(0.05)
>>> b = norm.ppf(0.95)
>>> print(a, b)
-1.6448536269514729
1.6448536269514722
# pdf(x) : 확률분포의 x에 대한 확률
# cdf(x) : 확률분포의 x에 대한 누적확률
>>> print(norm.pdf(a))
>>> print(norm.pdf(b))
>>> print(norm.cdf(a))
>>> print(norm.cdf(b))
0.10313564037537128
0.10313564037537139
0.049999999999999975
0.95
>>> c = [a,b]
>>> print(norm.cdf(c))
[0.05, 0.95]@staticmethod
def _poi(x, gp, y_max, xi):
with warnings.catch_warnings():
warnings.simplefilter("ignore")
mean, std = gp.predict(x, return_std=True)
z = (mean - y_max - xi)/std
return norm.cdf(z)POI는 EI와는 또 다른 Acquistion function이다.
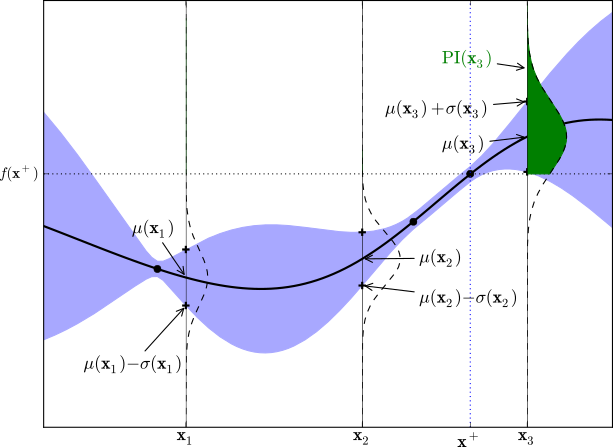
어느 후보 입력값 $x$ 에 대하여, ‘현재까지 조사된 점들의 함숫값 $f({x_1}),...,f({x_t})$ 중 최대 함수값 $f (x^{+})$ 를 우리는 최댓값 $max_i f(x_i)$라고 할 때, 이 최댓값보다 더 큰 함숫값을 도출할 확률(Probability of Improvement; 이하 POI)’ 이라 한다.
즉, 현재까지 조사된 점들의 함숫값 중 최대 함숫값보다 더 큰 함숫값을 도출할 확률’만을 반영한 Acquisition Function을 Probability of Improvement(POI)라고 한다.
- y_max와 std를 기준으로 mean의 Z 인자를 뱉어낸다.
- xi는 y_max를 어느정도 이동시키는 역할을 한다.
- max 값과 $f(x^+)$ 간의 차이 값(magnitude)이 클수록 Z는 음수에서 양수로 값은 계속 커질 것이다. 이 말은 y_max보다 계속 커질 것이라는 의미이다.
- 종합적으로 고려하여, Acquisition Function은 PI가 가장 높은 구간을 우리는 선택할 것이다. 이는 max 값보다 더 큰 값을 찾을 확률이 높다는 것을 의미한다. --> 이것은 POI에서 이 개념이 끝난다.
2. Expected Improvement
@staticmethod
def _ei(x, gp, y_max, xi):
with warnings.catch_warnings():
warnings.simplefilter("ignore")
mean, std = gp.predict(x, return_std=True)
z = (mean - y_max - xi)/std
return (mean - y_max - xi) * norm.cdf(z) + std * norm.pdf(z)EOI 는 POI에서 계산한 PI 값에서 지금 max인 값과 max로 예상되는 값의 차이만큼 가중하여 다음에 시행할 EI를 최종적으로 계산한다. 기존 점들보다 더 큰 함숫값을 얻을 확률도 중요하지만, 얼마나 큰 값을 얻을지도 굉장히 중요하기 때문이다.
<POI 개념을 업그레이드 한, 이 부분 진짜 매우 매우 중요하다.>
- y_max와 std를 기준으로 mean의 Z 인자를 뱉어낸다.
- xi는 y_max를 어느정도 이동시키는 역할을 한다.
- max 값과 $f(x^+)$ 간의 차이 값(magnitude)이 클수록 Z는 음수에서 양수로 값은 계속 커질 것이다. 앞에 mean-y_max-xi를 곱해주는 이유는 mean과 y_max와 차이가 많이 날 수록 global maximum이라는 정보를 입증하는 수치이다. 그래서 Z가 클 수록 y_max보다 mean이 크다는 의미이므로 가중치를 높여준다. (Exploitation)
- Z값을 가지는 위치에 존재할 때의 확률에서, std가 클수록 불확실한 구간이기에 곱해주어, exploration을 해준다. (exploration 전략)
종합적으로 고려하여, Acquisition Function은 Exploitation + Exploration이 둘 다 들어가게 된다.
$$\begin{align} EI(x) & = \mathbb{E} [\max (f(x) - f(x^{+}), 0)] \\ & = \begin{cases} (\mu(\boldsymbol{x}) - f(\boldsymbol{x}^{+})-\xi)\Phi(Z) + \sigma(\boldsymbol{x})\phi(Z) & \text{if}\ \sigma(\boldsymbol{x}) > 0 \\ 0 & \text{if}\ \sigma(\boldsymbol{x}) = 0 \end{cases} \end{align}$$
$$Z = \begin{cases} \frac{\mu(\boldsymbol{x})-f(\boldsymbol{x}^{+})-\xi}{\sigma(\boldsymbol{x})} & \text{if}\ \sigma(\boldsymbol{x}) > 0 \\ 0 & \text{if}\ \sigma(\boldsymbol{x}) = 0 \end{cases}$$
위의 계산을 따라가라면 아래의 링크를 타고들어가서 수학적 접근은 수식을 참고하자.
(참고로 공부해보다 느낀건데, 누적정규분포를 쓴거는, 위의 사진에서 PI(X3)를 구하려면 f(x+) 위에를 적분을 해야하는데, 적분 대신 Z를 누적정규분포로 해버리면, 누적정규분포의 f(x+) 지점에서의 y값은 f(x+) 까지의 적분한 표준정규분포의 값과 일치한다.)
ash-aldujaili.github.io/blog/2018/02/01/ei/
Expected Improvement for Bayesian Optimization: A Derivation
In this post, we derive the closed-form expression of the Expected Improvement $($EI$)$ criterion commonly used in Bayesian Optimization. Modelled with a Gaussian Process, the function value at a given point $x$ can be considered as a normal random variabl
ash-aldujaili.github.io
3. Entropy Search

@staticmethod
def _es(x, gp):
"""Entropy Search"""
with warnings.catch_warnings():
warnings.simplefilter("ignore")
_, std = gp.predict(x, return_std=True)
return std말 그대로, 엔트로피가 제일 낮은 구간, 즉 우리가 제일 모르는 미지의 구간을 찾는 것을 Entropy Search라고 말한다.
하지만 우리는 엔트로피를 측정하는 메소드가 없기 때문에, 엔트로피를 증빙하는 std, 편차를 이용해서, 각 x의 지점마다 편차가 높은 x는 그만큼 편차가 심하고, 가질 수 있는 값의 폭이 크다는 것을 의미, 이는 불확실한 구간을 의미한다.
따라서 편차가 높은 x를 찾아서 뱉어내게 된다.
4. Upper Confidence Bound

@staticmethod
def _ucb(x, gp, kappa):
"""Upper Confidence Bound"""
with warnings.catch_warnings():
warnings.simplefilter("ignore")
mean, std = gp.predict(x, return_std=True)
return mean + kappa * stdreturn 한 부분을 보면, mean에서 std를 hyperparameter인 kappa를 곱해준다. 이 의미는, 확률적으로 나가가는 것이 아니라, 단순히 x라는 지점에 대한 가우시안 분포가 제일 최고 지점을 찍는 부분을 return 하게 된다는 의미이다.
그림에서 초록색 가우시안 분포를 보면 된다. UCB를 하게 된다면, 초록색 가우시안 분포에서 제일 위 끝 지점의 값이라고 생각하면 된다.
Bayesian Optimization의 단계 (그냥 읽어보기)
- 입력값, 목적 함수 및 그 외 설정값들을 정의합니다.
- 입력값 x: 학습률
- 목적 함수 f(x): 설정한 학습률을 적용하여 학습한 딥러닝 모델의 검증 데이터셋에 대한 성능 결과 수치(e.g. 정확도)
- 입력값 x의 탐색 대상 구간: (a,b).
- 맨 처음에 조사할 입력값-함숫값 점들의 갯수: n
- 맨 마지막 차례까지 조사할 입력값-함숫값 점들의 최대 갯수: N
- 설정한 탐색 대상 구간 (a,b) 내에서 처음 nn개의 입력값들을 랜덤하게 샘플링하여 선택합니다.
- -----------------------------------------------------------------------------------------------------------------
- 선택한 nn개의 입력값 x1,x2,...,xn을 각각 학습률 값으로 설정하여 딥러닝 모델을 학습한 뒤, 검증 데이터셋을 사용하여 학습이 완료된 모델의 성능 결과 수치를 계산합니다. 이들을 각각 함숫값 f(x1),f(x2),...,f(xn)으로 간주합니다.
- 입력값-함숫값 점들의 모음 (x1,f(x1)),(x2,f(x2)),...,(xn,f(xn))에 대하여 Surrogate Model로 확률적 추정을 수행합니다.
- 조사된 입력값-함숫값 점들이 총 NN개에 도달할 때까지, 아래의 과정을 t=n,n+1,...,N−1에 대하여 반복적으로 수행합니다.
- 기존 입력값-함숫값 점들의 모음 (x1,f(x1)),(x2,f(x2)),...,(xt,f(xt))에 대한 Surrogate Model의 확률적 추정 결과를 바탕으로, 입력값 구간 (a,b) 내에서의 EI의 값을 계산하고, 그 값이 가장 큰 점을 다음 입력값 후보 xt+1로 선정합니다.
- 다음 입력값 후보 xt+1을 학습률 값으로 설정하여 딥러닝 모델을 학습한 뒤, 검증 데이터셋을 사용하여 학습이 완료된 모델의 성능 결과 수치를 계산하고 이를 f(xt+1)값으로 간주합니다.
- 새로운 점 (xt+1,f(xt+1))을 기존 입력값-함숫값 점들의 모음에 추가하고, 갱신된 점들의 모음에 대하여 Surrogate Model로 확률적 추정을 다시 수행합니다.
- 총 N개의 입력값-함숫값 점들에 대하여 확률적으로 추정된 목적 함수 결과물을 바탕으로, 평균 함수 μ(x)을 최대로 만드는 최적해 x∗를 최종 선택합니다. 추후 해당 x∗ 값을 학습률로 사용하여 딥러닝 모델을 학습하면, 일반화 성능이 극대화된 모델을 얻을 수 있습니다.
Summary

목적
결국 Bayesian Optimization은 surrogate model을 우리가 얻고자 하는 MAX나 MIN을 위해 random sampling에 기반하여 data를 최대한 효율적으로 sampling을 하여 점점 우리의 acquistion function을 기반으로 Maximum value를 도출해낸다.
Model
Bayesian Optimization은 Gaussian Process Prior을 기반으로 하며, $p(f) = GP(f; μ,K)$ 라고 정의한다.
그리고 obseravation $D=(X,f)$라는 분포를 써서 $p(f|D) = GP(f: μ_{f|D}, K_{f|D})$ , 즉 posterior 분포를 만들어서 실제 데이터를 기반으로 다음 step을 예측한다.
다음 step을 예측할 때는 acquistion function에 기반하여 다음 step을 정하는 decision making을 하게된다.
성능
즉, acquistion function을 어떤 것을 쓰느냐, xi (EI, POI)와 kappa (UCB만 해당)를 어떻게 설정하느냐에 따라 Bayesian Optimization의 성능이 달라진다.
Code에 적용하면 좋을 부분
docs.scipy.org/doc/scipy/reference/tutorial/optimize.html
Optimization (scipy.optimize) — SciPy v1.5.2 Reference Guide
The scipy.optimize package provides several commonly used optimization algorithms. A detailed listing is available: scipy.optimize (can also be found by help(scipy.optimize)). The minimize function provides a common interface to unconstrained and constrain
docs.scipy.org
Code
http://research.sualab.com/introduction/practice/2019/04/01/bayesian-optimization-overview-2.html
Bayesian Optimization 개요: 딥러닝 모델의 효과적인 hyperparameter 탐색 방법론 (2)
(이전 포스팅 보기)
research.sualab.com
Principle
http://research.sualab.com/introduction/practice/2019/02/19/bayesian-optimization-overview-1.html
Bayesian Optimization 개요: 딥러닝 모델의 효과적인 hyperparameter 탐색 방법론 (1)
지난 글의 서두에서 ‘AutoML’이라는 주제에 대해 간단히 소개해 드린 적이 있습니다. AutoML을 한 문장으로 표현하자면 ‘Machine Learning으�
research.sualab.com
RandomForest 적용한 Bayesian Optimization
ymattu.github.io/MlBayesOpt/reference/rf_opt.html
Bayesian Optimization for Random Forest — rf_opt • MlBayesOpt
This function estimates parameters for Random Forest based on bayesian optimization. rf_opt(train_data, train_label, test_data, test_label, num_tree = 500L, mtry_range = c(1L, ncol(train_data) - 1), min_node_size_range = c(1L, as.integer(sqrt(nrow(train_da
ymattu.github.io
'Optimization' 카테고리의 다른 글
| Optimization : Reference (0) | 2020.07.28 |
|---|---|
| Optimization : Genetic (0) | 2020.07.28 |
| Optimization : Heurisitc (0) | 2020.07.28 |
| Optimization : ABC (Artificial Bee Colony) algorithm (0) | 2020.07.21 |
| Optimization : 최적화 개요 (0) | 2020.07.21 |



댓글