DQN (Deep Q-Networks)

지금까지 우리가 배웠던 내용을 간단하게 정리해보자!

우리는 지금까지 Model을 알고 있는 경우를 Dynamic Planning으로 해결했으며,

Model을 모르는 경우는 한 episode가 끝난 이후에 Return Function을 계산하는 Monte Carlo Method 나

일정한 Term을 주고 한 episode에 대해서 Return Function을 계산하는 TD Method 방법이 존재했다.

또한 우리는 어떤 특정 state일 때, 가지는 누적 reward, Return들의 기댓값을 말하는 Value function을 찾는 것이 목적이다. 이 Value Function은 어떤 특정 state일 때, 특정 action 을 선택할 확률인 Policy, $\pi$와 특정 state에서 action을 취했을 때, 가지는 누적 Reward, Return 들의 기댓값을 Q-Function 을 곱한 값이다.

결국, 우리는 Value function을 찾는 것이 목적이지만, 현실적으로 모든 state 들에 대한 return 값들을 안다는 것은 모든 state에 대해서 test를 해봐야한다는 것이고, 이는 현실세계에서는 거의 불가능하다. 그래서 우리는 어떤 특정 state에서 policy에 근거하여 action을 취했을 때, 가지는 Return들의 기댓값을 말하는 Q-Function을 알아내어서 Value Function에 근사시키자는 개념이 나왔다. 이것을 우리는 Q-Learning이라고 한다.

여기까지가 우리가 지금까지 공부했던 방향이다.

하지만 역시나 Q-learning을 공부하면서 예시를 들었던 것은 언제나 작은 범위에 문제들이었고, 실제로 현실세계의 문제들은 예시문제들과는 천차만별 다르다. 실제로 변수들도 엄청 많고, 가질 수 있는 state들의 갯수만하더라도 수십, 수백만개이다. 결국 우리는 지금까지 우리가 배운 개념들을 실제 문제에 적용하기위해 많은 노력을 하고 있고, Q-learning을 하기 위한 table 을 만드는 것이 아니라, 이 부분을 Supervised Learning과 Un-Supervised Learning에서 이미 좋은 성능을 보였던 Deep Learning이 과연 Reinforcement Learning에서도 쉽게 적용이 될 것인가? 에 대한 물음에 답을 이 포스팅에서 하려한다.

실제로 DQN 은 구글의 DeepMind에서 Atari game 으로 낸 논문 에서 언급되었다.

실제로 Reinforcement Learning에 Deep Learning을 적용한 첫 사례라고 볼 수 있을 것이다.

DQN의 정의

We refer to convolutional network trained with our approach as Deep Q-Networks (DQN).

The model is a convolutional neural network, trained with a variant of Q-learning, whose input is raw pixels and whose output is a value function estimating future rewards.

간단히 말하자면, DQN은 어떤 특정 state에서 policy에 근거하여 action을 취했을 때, 가지는 Return들의 기댓값을 말하는 Q-Function을 알아내어서 Value Function에 근사시키자는 개념이 나왔다. 이것을 우리는 Q-Learning이라고 한다.

\begin{equation} Q^\pi(s, a) = \mathbb{E}_\pi \{R_t | s_t = s, a_t = a\} = \mathbb{E}_\pi \{\sum_{t'=t}^T \gamma^{t'-t} r_{t'} | s_t = s, a_t=a \} \end{equation}

위처럼 우리는 Q-Learning을 하기 위해서는 경험한 state에 대한 Q-Table을 가지고 있어야하는데, 우리는 Q-Table을 Deep Neural Network로 대체하겠다는 것이 바로 DQN이다.

DNN을 우선 Value Function, Q-Function을 표현할 때, 신경망을 적용했으며, Atari game의 화면을 CNN을 적용하였다. 그래서 왼쪽 그림대로 표현이 가능하고, 실제로 우리는 Loss Function을 현재 상태에서의 Q-Value를 예측하는 것이라고 정의하는 True Q-Function과 우리가 예측하는 Q-Function과의 차이를 MSE한 것으로 정의한다. 그리고 optimizer는 SGD를 이용해서 발산을 최대한 줄였다.

model free한 문제인 Atari Game의 단계들을 사진들의 Feature들을 모아서 Input으로 하고, output을 Value Function으로 하고 있다. 따라서, 경험된 데이터에서 학습하여, predicition을 하는 방법을 쓴다. 추정된 Value funciton은 future reward을 추정하는데 이용되는 재료가 될 것이다.

RL의 한계점

Recent breakthroughs in computer vision and speech recognition have relied on efficiently training
deep neural networks on very large training sets.
The most successful approaches are trained directly from the raw inputs, using lightweight updates based on stochastic gradient descent.
By feeding sufficient data into deep neural networks, it is often possible to learn better representations than handcrafted features [11]. These successes motivate our approach to reinforcement learning.
Our goal is to connect a reinforcement learning algorithm to a deep neural network which operates directly on RGB images and efficiently process training data by using stochastic gradient updates.

우선 RL 분야는 DQN 전 까지는 agent가 high-dimensional한 vision아나 data를 다루는 것은 매우 힘들었다. 그나마 agent가 다룰 수 있도록 feature들을 골라주면 가능했을 정도이다. 그래서 Deep Learning 분야에서도 high dimensional data를 다루는 CNN, RNN 등 여러가지 기법을 RL에 적용하고 싶어 하였다.

하지만, RL과 DL은 두 가지 차이점이 존재하여 같이 적용하기 매우 힘든 알고리즘이다.

RL과 DL 차이점

However, reinforcement learning presents several challenges from a deep learning perspective.
Firstly, most successful deep learning applications to date have required large amounts of handlabelled training data.
RL algorithms, on the other hand, must be able to learn from a scalar reward signal that is frequently sparse, noisy and delayed. The delay between actions and resulting rewards, which can be thousands of timesteps long, seems particularly daunting when compared to the direct association between inputs and targets found in supervised learning.
Another issue is that most deep learning algorithms assume the data samples to be independent, while in reinforcement learning one typically encounters sequences of highly correlated states.
Furthermore, in RL the data distribution changes as the algorithm learns new behaviours, which can be problematic for deep learning methods that assume a fixed underlying distribution.

첫 번째로, RL은 Hand-Labelled Data를 쓰지 않고, 오로지 경험과 reward에 근거하여 학습한다는 것이다.

Deep Learning은 지금까지는 Supervised Learning에서 돋보적인 성능을 보여왔고, Supervised Learning은 hand-labelled data를 필수적으로 입력을 해주어야한다. 여기서 hand labelled data 의 의미는, 변수가 존재하고, y값이 확실하게 존재하는 data들의 특성을 말한다. 하지만, Reinforcement Learning은 오로지 reward를 기준으로 학습이 진행되고, 그 reward도 굉장히 복잡한 절차를 걸치며 sparse하고 거의 같은 reward가 없기 때문에 noisy하며, 매 episode 마다 갖는 step이 매번 다르기 때문에, delay된다. 즉, data의 sequence가 매 episode마다 천차만별이 될 수 밖에 없다는 것이다.

두 번째로, RL에 들어가는 data들은 서로 엄청난 correlation을 가질 수 밖에 없다는 것이다.

Deep Learning에 들어가는 data들은 서로 독립일 것이다. 개의 사진, 고양이의 사진, 등등 여러가지 동물의 사진이 있고, 이를 NN가 학습할 경우, 개의 사진을 학습한 모델이 고양이의 사진을 판별할 때 영향을 끼치지는 않는다는 것이다. 즉, 동물들의 data는 서로의 data에 영향을 주지 않는다는 것이다.

하지만 Reinforcement Learning은 다르다. 애초에 state, action, reward 3가지 개념이 존재하고, state에서 action을 취해서 reward를 받고, 다음 state 는 전 단계의 state에 영향을 받는다고 말할 수 있기 때문에, 다음 state의 reward는 처음 state의 reward에 영향이 끼칠 수 밖에 없고, correlation이 있다고 말할 수 있다.

Idea : Experience Replay

목적

인접한 학습데이터 사이의 correlation으로 인한 비효율성을 줄이기 위함이다.

이전에 살펴본 algorithm들과 같이 본 논문이 나오기 전에는 environment와 상호작용하며 얻어진 on-policy sample들,

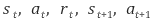
을 통해 parameter를 update하였다. 하지만, 이와 같은 방법은 on-policy sample을 통해 update하기때문에 sample에 대한 의존성이 커서 policy가 converge하지 못하고 oscillate할 수 있다. 그리고 그 전에는 한 episode 당 한 번 update를 하면 state들의 value function 을 업데이트 했고, 그 data는 다음 episode에서 쓰이지 않았기 때문에 data 재사용이 어려웠다. 이러한 문제를 해결하고자, 착안한 아이디어가 Experience replay다.

방법

각 time-step별로 얻은 sample(experience) data 들을 아래와 같은 tuple형태로 replay memory라는 buffer pool에 저장해두고, randomly draw하여 mini-batch를 구성하고 update하는 방법입니다.

이 때, data set은 무한히 저장할 수 없기 때문에 N으로 고정하고, FIFO방식(?) 으로 들어온 순서대로 저장한다. 논문의 실험에서는 replay memory size를 1,000,000으로 설정한다. 이렇게 tuple 형태로 저장한 후, mini batch size를 정하면, 그 만큼 dataset에 남아있던 data 를 batch size 만큼 random하게 뽑아낸다. 즉, dataset간에 sequence에 영향을 받지 않게 되기 때문에, data간의 correlation을 최대한 줄일 수 있다는 것이다.

장점

data sample을 한번 update하고 버리는 기존의 방법과 달리 경험데이터를 담아두고, random sampling을 함으로써 data usage efficiency를 도모할 수 있다.
RL에서 발생할 수 있는 state간의 high correlation 문제를 해결 할 수 있다.
SGD를 써서 불필요한 feedback loops를 돌거나, parameter들이 local minimum에 빠지거나 diverge하는 경우를 찾아낼 수 있어서, 이를 방지할 수 있다.
주의할 점은, experience replay를 사용할 땐, 반드시 off-policy로 learning해야하는데, 이는 current parameter가 update하는 sample들과 다르기 때문이다.

Idea : Target Network, Fixed Q-target

목적

Q-Function을 학습하는 과정에서 target 값도 변하게 되면서 기존의 정보를 잃지 않도록 하는 것이다. (transfer learning과 유사하다)

DQN에서 Q-Function을 추정하는 NN과 Target을 나타내는 NN을 분리해서, Q-Target NN의 weight 값을 가끔씩 Update 하도록 한 것이다. Target Network의 weight 값들은 주기적으로 DQN의 값을 복사해온다.

\begin{equation} L_i(\theta_i) = \mathbb{E}_{(s,a,r,s') \sim U(D)} \left[ \left( {r + \gamma \max_{a'} Q(s', a';\theta_i^-) - Q(s, a;\theta_i)} \right)^2 \right] \end{equation}

이는 Q-learning target $y_{i} = r + γ m a x_{a^{'}} Q (s^{'}, a^{'}; θ_{i})$ 를 근사하는 $Q (s, a; θ_{i})$ 를 구하려는 것과 같다. 문제는 yi 가 Q-Function에 대해 의존성을 갖고 있으므로 Q-Function를 업데이트하게 되면 target yi 또한 움직이게 된다는 것이다. 이 현상으로 인한 학습의 불안정함을 줄이기 위해 fixed Q-targets를 이용한다.

방법

jsideas.net/dqn/

Review: Deep Q Learning

a novice's journey into data science

jsideas.net

여기서 Fixed Q-Target 에 대해 자세히 적어놓은 설명이 있어 요역해서 적어보려한다.

사람이 낚시대에 당근을 걸어두고 당나귀 앞에 두면, 우리는 상식적으로 그 당근을 보며 당나귀가 일자로 갈거라고 생각한다. 하지만, 실상은 절대 그렇지 않다. 당나귀, 사람, 낚시대와 당나귀는 서로 연결되어있기 때문에, 당나귀가 움직인다면, 사람이 흔들리고, 낚시대와 당근이 흔들리게 되기 때문에, 그 당근을 보고 당나귀는 일자로 가지않고, 살짝 흔들리게 걸을 것이다.

당근의 위치를 Q함수의 타겟 \begin{equation} ( $r + m a x_{a^{'}} Q (s^{'}, a^{'})$ )\end{equation} 으로, 당나귀의 움직임을 추정치( $Q$ )로 대입해보면 된다. 타겟과 추정치의 오차를 줄여야하는데, $Q$ 의 변화에 따라 타겟과 추정치가 모두 함께 변화하면 안정적인 학습(이동)이 어려워진다.

DQN에서는 당나귀와 당근을 분리시키는 Fixed Q Targets 방법을 사용해서 문제를 해결한다. Q함수를 추정하는 네트워크(local network)와 Target을 설정하는데 사용하는 네트워크(target network)로 추정과 평가를 분리한다. 당나귀 등에서 내려서 낚시대를 드리우면, 당근의 위치는 더이상 당나귀의 움직임에 영향을 받지 않는다.

그리고 target network의 업데이트 주기를 local network보다 더 느리게 만듦으로써 목표가 자주 휘청이지 않도록 한다. DQN 구현에서는 local network가 4번 업데이트될 때 한번씩 target network의 파라미터를 local network의 파라미터를 사용해 soft update한다.

Idea : Gradient clipping

Network의 loss function $(r + γ m a x_{a^{'}} Q (s^{'}, a^{'}; θ_{i}^{-} - Q (s, a; θ_{i}))^{2}$ 에 대한 gradient가 -1 보다 작을때는 -1로, 1보다 클때는 1로 clipping해준다. 이러한 방식은 loss function이 일정 구간 내에서는 L2로, 구간 바깥에서는 L1으로 동작하게 하는데, 이는 outlier에 강한 성질이 있으므로 학습과정을 좀 더 안정적으로 만들 수 있다. Huber loss와 기능적으로 동일하기 때문에 구현시에는 loss function을 Huber loss로 정의하기도 한다.

Pseudo Code

finite capacity N을 가진 replay memory D를 정의하고 Q-learning을 위해 Q-value를 initialize 시킨다. 1 episode동안 sequence를 initialize시키고 pre-process 시킨다.

Pre-processing

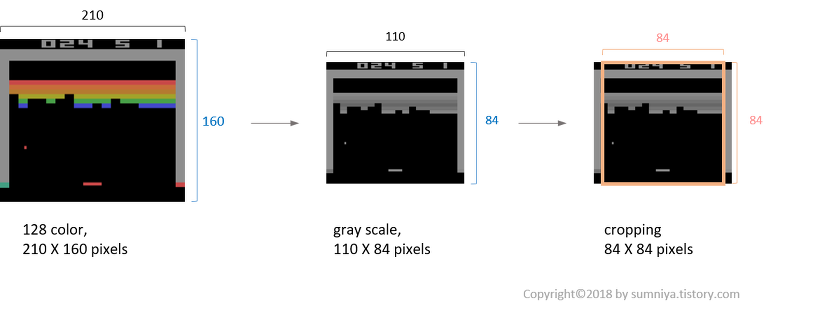
Atari 2600은 210x160 pixel의 colour image를 초당 60프레임 정도로 화면에 출력한다. 출력된 화면에 대해 다음과 같은 전처리 과정을 거쳐 84x84xm의 입력데이터를 얻는다[6]. (논문에서는 m을 4로 설정)

이미지의 크기를 (210, 160)에서 (84, 84)로 변환
RGB 이미지를 grayscale로 변환
연속된 이미지들 중 매 k번째에 위치한 이미지들만 선택된다(Skipped frame).*
3에서 선택된 이미지와 그 앞에 위치한 이미지에 대해 pixel-wise(component-wise) maximum을 취해준다.**
1-4의 과정을 거친 이미지들을 m개 만큼 쌓으면 네트워크의 입력으로 사용될 수 있는 하나의 상태(state)가 된다.***

*모든 frame을 전부 입력으로 활용하는 것은 자원 낭비이기 때문이다. 매 k번째의 이미지만 입력으로 이용하고 skipped frame에서는 가장 마지막에 선택된 action이 반복된다. 논문에서는 k를 4로 설정했다.

**Atari 2600은 화면에 한 번에 표시할 수 있는 sprites가 단 5개 뿐이어서 짝수 프레임, 홀수 프레임에 번갈아서 표시하는 것으로 여러개의 sprites를 화면에 보여줄 수 있었다. 연속된 두 이미지에 대해 component-wise maximum을 취해줌으로써 이를 한 이미지에 모두 표시할 수 있다.

***1-4의 과정을 거쳐서 얻은 이미지가 $x_{1}, x_{2}, \dots, x_{7}$ 이라고 했을때 s1=( $x_{1}, x_{2}, x_{3}, x_{4}$ ), s2=( $x_{2}, x_{3}, x_{4}, x_{5}$ ), $\dots$ , s4=( $x_{4}, x_{5}, x_{6}, x_{7}$ ). 즉, 연속된 states 간에는 overlapping이 발생한다.

Architecture

Frame이 4인 이유

last 4 Frame을 stack으로 쌓는다고 하는데, 여기서 frame은 Atari Game의 image는 초당 60 frame 정도로 화면에 출력한다. 이 때, 연속된 이미들 중 매 k번째에 위치한 이미지들만 선택된다. 여기서 모든 60개의 frame을 전부 입력으로 활용하는 것은 자원 낭비라고 말을 한다. 따라서 매 k 번째의 이미지만 입력으로 이용하고 논문에서는 k를 4로 설정했다.

Input & Output

Input state 는 이전의 $84 \times 84$ 크기의 프레임 4장이고, Output은 18개의 joystick/button 동작에 대한 $Q (s, a)$ 값, Reward는 score의 변경 값입니다.

저작자표시

'AI' 카테고리의 다른 글

Pytorch + RTX3080 (1)	2021.03.08
RTX 3080 병렬로 tensorflow 위에 올려보기 (0)	2020.12.23
Off-Policy Control (0)	2020.09.24
RL : RL 용어정리 (0)	2020.09.08
RL : TD Method (0)	2020.09.06

월곡동 로봇팔의 대학원일지