K-Nearest-Neighbor, KNN
목적, 정의

위와 같은 그림1에서 우리는 초록색 원이 세모인지, 네모인지를 구별하는 모델을 만들 것 이다.
이 때, 실선을 기준으로 모델을 만든다면, (k=3) 초록색 원이 세모일 것이라고 판단할 것이다.
하지만, 점선을 기준으로 모델을 만든다면, (k=5) 초록색 원은 네모가 더 많기 때문에 네모라고 판단할 것이다.
- 원 주위에 있는 갯수들, k까지를 선으로 긋는 모델을 정해줌으로써 모델을 만들 수가 있다.
- 또한 여기에 떨어진 거리를 weight를 주어, category를 판별할 수 있다.
이처럼 k의 갯수를 조정, 거리에 따른 weight를 조정해서 model을 만드는 것을 K-Neighbor-Nearest, KNN이다.
k, weight 수치 결정
- 너무 큰 k 라면 : 선 안에 있는 data의 갯수가 많기 때문에, 미세한 경계부분을 잘못 분류할 것

- 너무 작은 k 라면 : 선 안에 있는 data의 갯수가 적기 때문에, 그 category에 포함되지 않는 data인데 category에 포함시키는 오류를 범할 수도 있다. 또한 패턴이 직관적이지 않을 것-> 즉 overfitting이 일어날 수 있다.
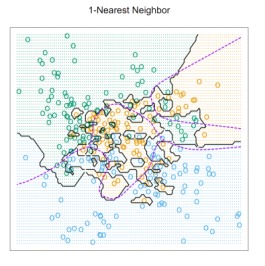
- 위에 그림에서 Blue가 훨씬 많았다면? : 거리가 멀수록 weight를 적게, 거리가 가까울수록 weight를 크게 주어서, 가까이 있는 data들을 더 우대하는 방향으로 해야한다.
- 중요한 변수, 불필요한 변수가 섞여있다면? : 중요한 변수만 선별할 필요가 있음.
변수
범주형 변수
- 근처 k개 중 가장 많이 나타나는 범주를 y로 추정.
- k를 홀수로 해야한다. 짝수면 두 개의 확률이 50:50으로 정해져 classify를 못한다.
 pm은 m번째 범주에 해당하는 data의 갯수/k, 즉 m범주에 해당하는 확률값이다. 또한 y hat은 그 pm들 중에서 제일 확률값이 높은 값이다.
pm은 m번째 범주에 해당하는 data의 갯수/k, 즉 m범주에 해당하는 확률값이다. 또한 y hat은 그 pm들 중에서 제일 확률값이 높은 값이다.- ex) 범주가 0,1,2 일 때, 확률이 0.5, 0.3, 0.2 // y hat은 0.5이다.
연속형 변수
- 근처 k개 중, KNN의 대표값(평균)으로 y로 추정.
 KNN의 평균, 대표값으로 y hat을 추정하는 식이다. 밑에처럼 weight를 주어 할 수도 있다.
KNN의 평균, 대표값으로 y hat을 추정하는 식이다. 밑에처럼 weight를 주어 할 수도 있다.- Inverse Distance Weighted Average 고려 가능. (거리가 가까울수록 weight 많이, 멀수록 weight 적게)
 위의 식에 거리를 반비례하는 식을 넣어주면 거리에 따라 weight를 준다.
위의 식에 거리를 반비례하는 식을 넣어주면 거리에 따라 weight를 준다.
Cross Validation
목적

위의 그림을 보았을 때, Bayes 정리에 의한 Bayes Error는 data가 동일한 이상, 무조건 Error 율은 동일할 것 이다.
k=1 에서는 training set에서는 Error가 없으나, Test에서는 Error가 굉장히 많이 발생한다.
k를 늘리면 점점 Error가 줄어드는 듯 하나, 일정 k 이상으로는 Error가 약간 올라가면서 유지된다.
이는 우리가 Test Set을 나누면서, 데이터를 나눠야하므로 데이터의 소실이 발생하기 때문이다.
따라서 우리는 Cross Validation을 통해서, Training Set을 계속 바꿔주면서, Error를 과소추정하지 않고, Error를 최대한 낮추는 것이 목표다.
방법

위의 그림처럼, k-fold에서 k가 5일 때, 5개의 split을 나눈 후, fold1,2,3,4,5를 번갈아가면서 test set으로 바꿔준다.
KNN 단점 : 차원의 저주

차원의 저주란, 차원을 줄이거나 늘릴 때, data의 변수가 하나 더 추가함에 따라 data가 나타내는 특징이 달라질 수 있다.
위의 그림에서 처음 data들을 한 가지 변수로만 파악했을 때는 왼쪽에 모두 쏠려 있지만, 변수를 하나 더 추가해서 바라보았을 때, 사각형 위로 퍼져있기 때문에, 차원이 늘어남에 따라 보는 관점이 달라질 수 있다. 이는 차원이 축소해도 마찬가지이다.

위와 같은 예시에서, x축에 정사영을 모두 내렸을 때, 5-NN을 살펴보면, 직사각형 안에 들어가 있는 초록색4개, 빨간색 1개여서, 검은색점은 초록색 점이라고 classify를 할 수 있다.
하지만, 차원을 늘려서 본다면, 5-NN은 원을 기준으로 판단하고, 빨간색 3개, 초록색 2개로 검은색 점은 빨간색 점이라고 classify를 할 수 있다.
따라서 차원을 늘리거나 축소할 때, 데이터가 유실될 수도 있어 이 부분은 각별히 조심해야한다.
'AI' 카테고리의 다른 글
| ML : Model : LDA : 사영(Projection) (0) | 2020.02.10 |
|---|---|
| ML : Model : LDA Math : 다변량 정규분포 (0) | 2020.02.10 |
| ML : Model : (Gaussian) Naive Bayes Classifier (0) | 2020.02.09 |
| ML : 오차 vs 잔차 (0) | 2020.02.01 |
| ML&DL : train, validation, test 데이터로 나누기 (0) | 2020.02.01 |



댓글