회귀분석
목적
1. 변수들이 서로 관련이 있는가?
2. 관련이 있다면 얼마나 밀접하게 관련이 있는가?
3. 관심이 있는 변수의 값을 그 외 다른 변수의 값으로부터 예측할 수 있는가? (머신러닝의 목적)
독립변수 & 종속변수
독립변수 (independent variable) : 실험하는 사람에 의해 통제되어 독립적으로 주어지는 변수
종속변수 (dependent variable) : 독립변수와 오차에 의해 결정되는 변수
우리는 산점도로부터 변수들 간에 대략적으로 직선의 관계라 있음을 알 수 있다.
하지만 대략적인 직선의 관계가 없더하더라도 변수의 적절한 변환을 통해서 직선의 관계를 만들 수 있다.
회귀분석은 D차원 벡터 독립 변수 xx와
이에 대응하는 스칼라 종속 변수 yy간의 관계를 정량적으로 찾아내는 작업이다.
공식
> 공식 : Yi = β0 + β1xi + εi, i = 1,2,3-----n
1. β0, β1 은 직선식을 결정하는 미지의 회귀모수이다.
2. 오차 εi 들은 서로 독립이며, 평균이 0, 분산이 σ**2 인 정규분포를 따른다. (εi 이기 때문에!!!!)
3. Yi는 독립변수를 xi로 고정시켰을 때의 종속변수의 값이다.

독립변수가 xi 일 때, 종속변수 Yi는 평균이 β0 + β1xi , 분산이 σ**2 , 인 정규분포를 따른다는 것을 알 수 있다.
이 의미는 Yi 는 εi 인 오차에 의해, 변동되는 것으로 볼 수 있다.
최소제곱추정법 (least squares method)을 이용한 모수 측정

위의 그림에서 점과 직선사이의 거리를 d라고 하자.
d = yi - (b0 + b1xi) 이것을 편차라고 하고 n개의 관측값이 있다고 할 때, 편차제곱합들의 합은 이 y=b0 + b1xi이 자료의 직선관계를 얼마나 잘 표현하는 것인지에 대한 수치를 나타내준다.
따라서 D를 최소화하는 b0, b1을 찾게되는데 이 값을 최소제곱추정량이라고 하고, β0 hat, β1hat 이라고 한다.
또한 y hat = β0 hat + β1hat x 를 추정회귀직선이라고 한다.

잔차제곱합 (SSE, sum of squares due to error) = ∑ei**2 = Syy - Sxy**2/Sxx
평균제곱오차 (MSE) = 오차의 분산 σ**2의 추정량 = σ**2 = SSE / (n-2) // σ**2이 ∑ (y - yhat)
n-2로 나누는 이유는 두 개의 모수 β0, β1을 추정하고 남은 n-2가 SSE의 자유도이기 때문이다.
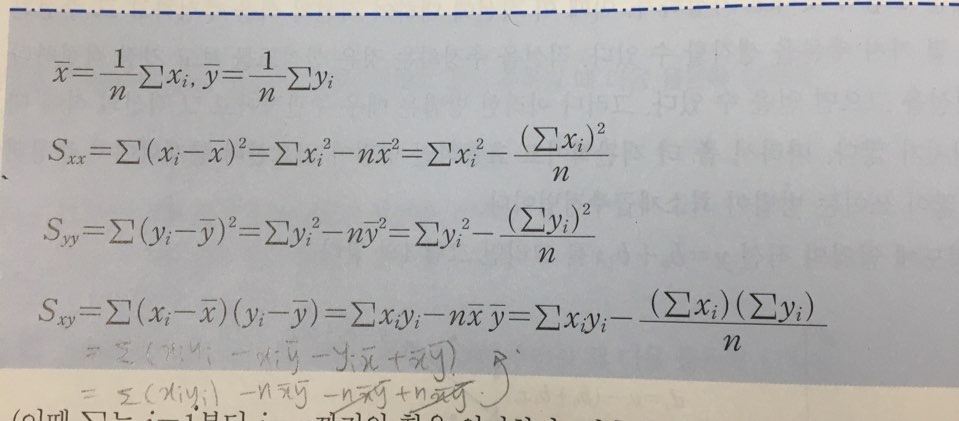
cf) 위에서 Sxx를 구하는데, ∑(xi * xbar) ->∑xi = n xbar
위의 추정량을 이용해서 β0, β1을 구해보자
β0 hat = y bar - β1 hat * x bar
β1 hat = Sxy / Sxx

출처 : https://statnmath.tistory.com/40
(개념&증명) 2. 단순회기분석에서 기울기와 절편은 어떻게 구할까 - Least Squares Method
그 전 포스팅에서는 함수적인 관계와 통계적인 관계의 차이점을 잠시 설명드렸어요. 함수적인 관계는 X값을 넣으면 Y값이 딱 나오는걸 말하지만, 통계적인 관계는 오차가 있기 때문에 X값을 넣으면 Y값이 딱 나오..
statnmath.tistory.com
예시 - 1
| 3 | 3 | 4 | 5 | 6 | 6 | 7 | 8 | 8 | 9 |
| 9 | 5 | 12 | 9 | 14 | 16 | 22 | 18 | 24 | 22 |
Q . 위가 복용량 x, 아래가 효과지속기간 y 이다.
위들의 산점도를 토대로 단순선형회귀모형에서의 모수를 측정하여 추정회귀직선을 구하고, 자료에서 주어진 각 복용량에 대한 지속기간의 추정량, 잔차, 오차분산의 추정량을 구하라.
Xbar = 5.9, Ybar = 15.1
Sxx = 389 - 59**2/10 = 40.9
Syy = 2651 - 151**2/10 = 370.9
Sxy = 1003 - 59*151/10 = 112.1
β1 hat = Sxy/Sxx = 2.74
β0 hat = ybar - β1 hat * xbar = -1.07
SSE = ∑ei**2 = Syy - Sxy**2/Sxx = 63.653
MSE = SSE/(n-2) = 7.96
'AI' 카테고리의 다른 글
| Statistics : 선형회귀 : 잔차의 검토 (0) | 2020.01.14 |
|---|---|
| Statistics : 회귀분석 : 선형관계의 강도 (0) | 2020.01.14 |
| Statistics : 정규모집단에서의 추론 : t 분포 (0) | 2020.01.11 |
| Statistics : 10-4 : 모비율에 대한 추론 (표본의 크기가 클 때) (0) | 2020.01.11 |
| Statistics : 10-3 : 통계적 추정 : 가설검증 (가설의 정의, 오류의 종류) (0) | 2020.01.11 |




댓글