
Marginal Likelihood는 두 가지 관점에서 이야기할 수 있는데, 첫 번째는 말그대로 marginalize 하여 가능도를 구한다는 개념으로 어떠한 파라미터를 지정해서 그것에 대한 가능도를 구하면서 나머지 파라미터들은 marginalize 하면 된다. (marginalize 한다는 것은 영어로는 marginalized out == integrated out 이라고 표현한다) 두 번째로는 베이지안 관점에서는 단지 베이즈 이론에서 Evidence에 해당하는 즉, 데이터에 대한 확률 부분을 일컫는 말이다. 왜냐하면 사실 이 부분은 데이터의 확률을 구하기 위해서 위의 그림에서 그려진 오른쪽 항의 분자를 marginalize 하기 때문이다.
내가 이해한 부분
기존 data가 존재하고 , θ라는 parameter가 존재할 때, α라는 새로운 parameter가 한다면 그 때 data를 예측할 확률이다. 즉 P(X|α) 이다.
즉, 이 수치는 기존 data를 반영해서 만든 모델이 새로운 parameter, α를 반영할 때, α가 과연 기존 data를 얼마나 잘 표현할 수 있는지에 대한 지표라고 생각한다.
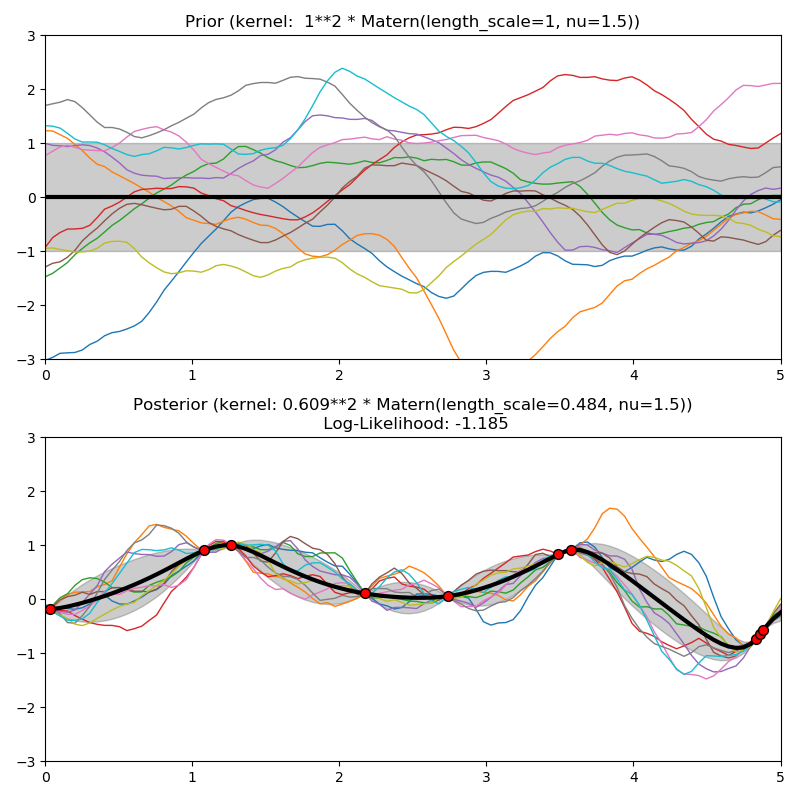
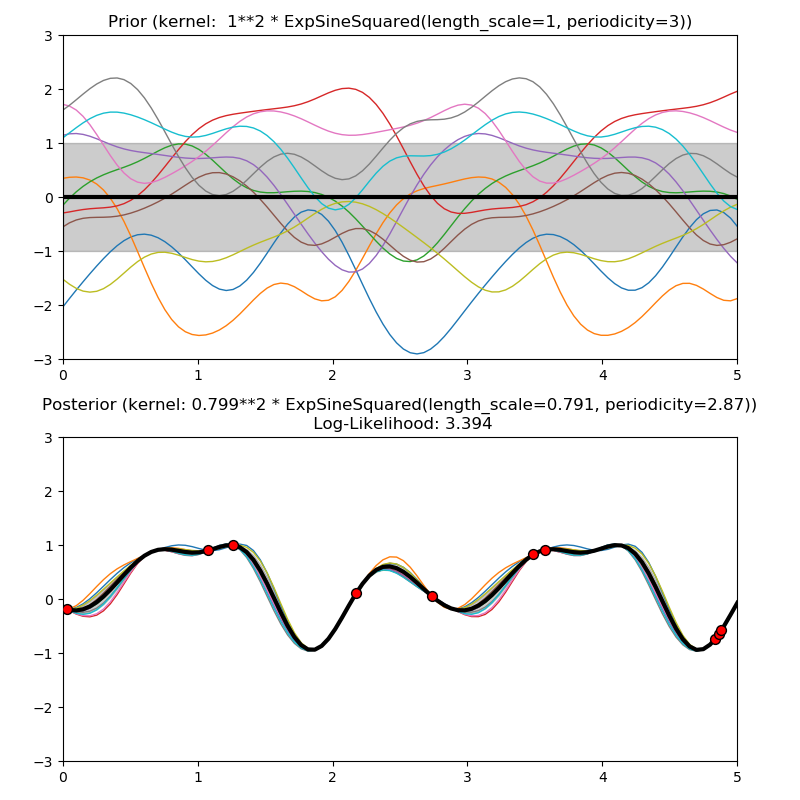
위의 그래프를 보면, log-likelihood가 왼쪽은 -, 오른쪽은 + 값으로 차이가 많이 난다. 이 말은 오른쪽 그래프가 양의 값을 가지니, 기존 data를 이용해서 함수를 만들었을 때, 여러 값을 주어도, 편차가 심하지 않게 mean 에 대한 함수로 귀결되는 것을 볼 수 있다.
즉, log-likelihood가 클수록 data를 잘 표현하는 함수를 만들었다고 봐도 가능하다.
출처:
[수리통계학] Marginal Likelihood 란? (빈도주의VS. 베이지안 관점 비교)
Marginal Likelihood (or Integrated Likelihood)에 대해서 알아보겠다. 항상 그랬듯이 먼저 위키 정의...
blog.naver.com
https://donghwa-kim.github.io/Pred_-baye.html
Prior & Posterior Predictive Distributions
Observed Case Prior distribution($p(\theta)$): 데이터를 알기 전에 분포 Posterior distribution($p(\theta | y)$): 데이터를 알고 난 후의 분포 앞서 배운 위의 분포들은 현재 학습데이터에 대한 분포로, unobserved data에
donghwa-kim.github.io
https://en.wikipedia.org/wiki/Posterior_probability
Posterior probability - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Conditional probability distribution used in Bayesian statistics In Bayesian statistics, the posterior probability of a random event or an uncertain proposition[clarification needed] i
en.wikipedia.org
'AI' 카테고리의 다른 글
| ML : Gaussian Process's Kernel (0) | 2020.06.08 |
|---|---|
| ML : Gaussian Process (0) | 2020.06.04 |
| Statistics : Posterior, Prior, Likelihood (0) | 2020.06.04 |
| ML : Prior Posterior (0) | 2020.05.29 |
| ML : sklearn : PolynomialFeatures (0) | 2020.05.22 |


댓글