Supervised vs UnSupervised
| Supervised | Unsupervised |
| (x : data, y : label) -> data를 보고 labeling을 함. | Just Data, X |
| Classification, Regression, Object Detection, Semantic Segmentation, Image Captioning |
Clustering (K-mean), Dimension Reduction (PCA, 3차원 공간에 있는 data들을 성분분석을 통해 2차원 공간으로 내려서 봄.)
Feature Learning (VAE, GAN : input data가 encoder NN을 통해 Feature Z라는 잠재변수를 만들고, Z를 이용해 다시 data를 만들어 처음 input data-output data의 차를 비교한다.)
Density Estimation |
| Goal : function을 map x->y | Goal : Data들의 Underlying Feature를 찾아내는 것. |
Goal
Data가 가지는 확률밀도함수가 존재하는데, model의 확률밀도함수를 Data가 가지는 확률밀도함수로 근사시키자!!
Why Generative Model?
- 연관성이 높지만, 없던 sample들을 많이 만들 수 있다. (강화학습에 도움.)
- 잠재변수 (우리는 모르는 변수) 들을 일반적인 변수로써 쓸 수 있다.
Generative Model's Structure
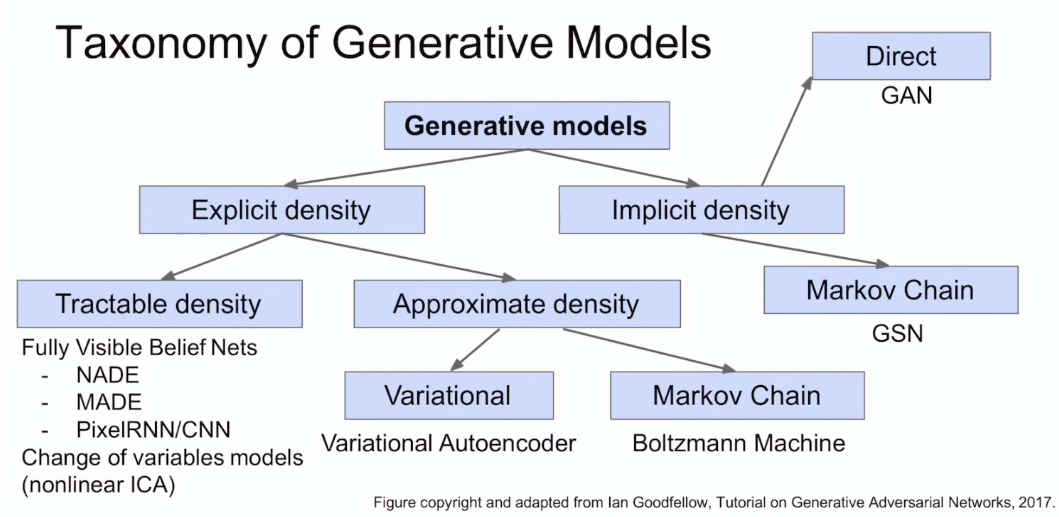
Explicit Density-Estimation : Pmodel 을 정확히 알고 정의할 수 있다.
Implicit Density-Estimation : Pmodel 을 식으로 정확히 모르지만, sampling은 할 수 있다.
AutoEncoder
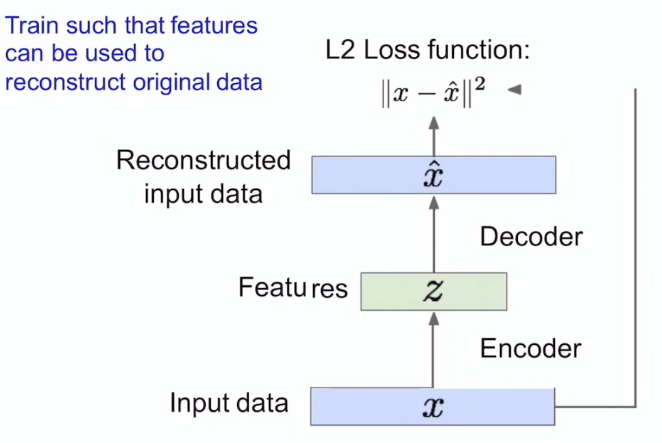
과정
- Input_data가 Encoder라는 NN을 통과해서 중요한 Feature를 얻은 후,
- 다시만든 input_data와 비슷한 결과값의 차이를 확인한 후, loss function의 값을 줄여나간다.
응용
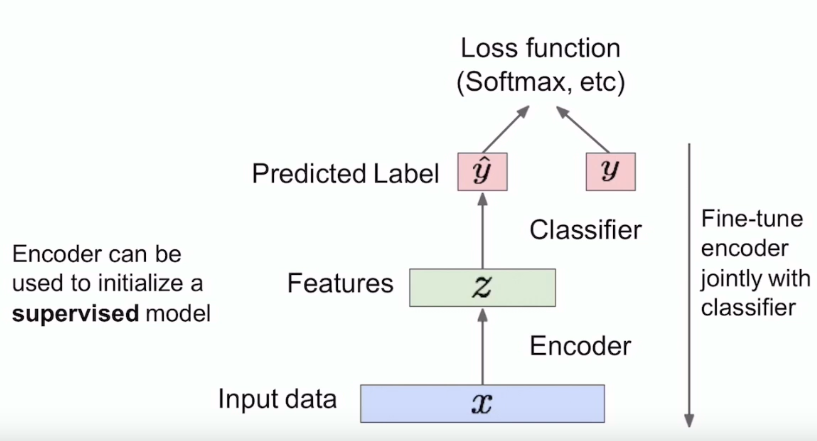
dataset이 적은 경우, data의 영향을 주는 feature를 뽑아서, 그 feature를 중심으로 classification을 진행한다면, 전체 x를 학습하는 것이 아닌, feature를 중심으로 학습을 하게되어, 적은 양으로도 training이 가능하다.
Varaitional AutoEncoder
Concept
AutoEncoder와는 다르게 input_data 와는 조금 다른 output_data를 만들어내며, AE에서처럼 특정한 벡터 z라고 지정하지 않고, z를 일정한 값이 아닌 분포로 띄게 하자.
중요한 feature의 parameter(모수)를 담고있는 Z 분포로 부터 vector를 random sampling을 하여, 이 분포의 오차를 이용하여 우리가 x라는 다양한 data를 만들어내는것을 VAE라고 한다.
목표
우리는 pθ(x) 를 x라는 data가 관측될 때, 최적인 parameter(모수, θ)가 나타내는 가능도함수의 pdf이다.
따라서 이 pdf의 maximun, MLE를 찾는 것이 우리가 찾고하는 x라는 data를 가장 관측할 확률이 높은 것을 측정하는 것이다.
그러기 위해 우리는 적절한 parameter, 모수,θ를 찾아야 한다.
과정

AE에서는 p(x) = p(x|z)이다.
하지만 VAE에서는 p(z)는 z가 특정벡터가 아니고 가능도함수, 분포이니 μ 일때가 가능도함수가 MLE, 제일확률이 높다.
따라서 μ 라는 모수를 안 상태에서 x라는 output data를 만들어내는 pdf를 pθ(x|z),
z분포를 이용하여 특정 벡터z, MLE 지점의 평균값, 특정벡터 z를 만들어내는 pdf를 pθ(z) 라고 한다.
이 때, Z를 가우시안 분포로 가정한다. (자연에 있는 분포들은 가우시안을 따른다. (얼굴표정은 무표정이 중간값이다.) )
output x는 엄청나게 고차원 배열이기 때문에 가우시안 분포로 가정을 할 수가 없다. 또한 Backpropagation을 할 때 미분이 되지 않기 때문에, 미분이 가능하게 정규분포로 가정한다. (reparameterization trick)
아래의 reparameterization trick을 공부해보자.
http://jaejunyoo.blogspot.com/2017/05/auto-encoding-variational-bayes-vae-3.html
초짜 대학원생의 입장에서 이해하는 Auto-Encoding Variational Bayes (VAE) (3)
Machine learning and research topics explained in beginner graduate's terms. 초짜 대학원생의 쉽게 풀어 설명하는 머신러닝
jaejunyoo.blogspot.com
따라서 NN을 통해 output의 x의 pdf를 근사를 해서 이를 p(x|z)라고 하자.
p(z) 함수를 가우시안 분포라고 가정을 했기 때문에 data가 주어질 때, 자료 x안에서의 최적의 parameter를 찾는 MLE (Maximun Likelihood Estimation)을 구한다면, p(z)와 p(x|z)의 parameter, θ을 구할 수 있다.
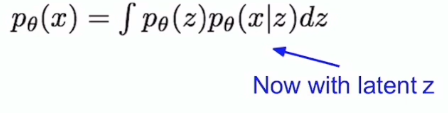

하지만 위의 그림처럼 data에 대한 likelihood 를 나타내는 p(x)를 구하려면 모든 z에 대해 적분을 해야해서 불가능하다.
z는 분포이기 때문에 무한으로 적분을 해야해서 힘들다.
p(z)p(x|z) dz 는 p(x,z)dz 와 같으므로 이를 적분하면 p(x)가 된다.
따라서 z는 분포이긴한데 p(z|x)에 대한 정보가 없다. 따라서 어떤 분포인지 성격도 모른다. 따라서 p(z|x)라는 증거를 주어서 p(x)를 구하려한다. 우리는 베이지안 룰을 적용해서 p(z|x)를 구하자. p(z|x)를 우리가 정한다면 p(x)를 쓸 수 있다.
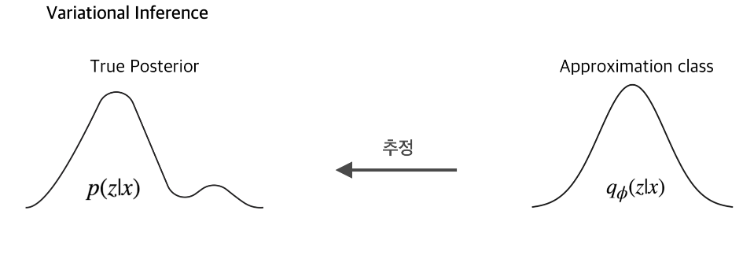
하지만, 여기서 p가 아니라 q인 이유는 p(z|x) 또한 정확히 모르기에 이를 q(z|x)라는 NN == 정규분포로 근사하자.
위에서 p(x|z)가 p인 경우는 z가 정규분포라고 가정을 했기 때문에, p(x|z)는 정규분포이고 그대로 p를 쓴다.
아까 p(x|z)는 decoder NN으로 구했으니, 이번에는 encoder NN으로 넣어서 근사시켜보자 라는 의미이다.
위에서 Variational Inference에서 정규분포를 가정한 이유는 KL을 계산하는데 있어서, 정규 분포 이외의 분포를 사용하면 두 분포 간의 KL을 모수 만을 사용하여 계산하기 까다롭기 때문이다.
Encoder code
그전에 Encoder는 어떻게 구성되는지 code로 살펴보자
from keras import metrics
from keras import layers
from keras.models import Model
from keras import backend as K
import numpy as np
# encoder
post_x = (28, 28, 1)
latent_dim = 2
input_layer = layers.Input(shape=img_shape)
# post_x라는 사진에서 feature인 x를 추출
post_x = layers.Conv2D(32, 3, padding='same', activation='relu')(input_layer)
post_x = layers.Conv2D(64, 3, padding='same', activation='relu', strides=(2, 2))(post_x)
post_x = layers.Conv2D(64, 3, padding='same', activation='relu')(post_x)
post_x = layers.Conv2D(64, 3, padding='same', activation='relu')(post_x)
# feature 들을 flatten 작업 -> shape를 1차원으로 만든다.
shape_before_flattening = K.int_shape(post_x)
flat = layers.Flatten()(post_x)
-----------------------------------------------------------------------------
# 여기서부터 VAE
# input x가 만들어짐
x = layers.Dense(32, activation='relu')(flat)
# 가정한 확률분포의 모수, 모수 추출하는 layer를 q(z|x)라 생각하자
z_mean = layers.Dense(latent_dim)(x)
z_log_var = layers.Dense(latent_dim)(x)Encoder는 말 그대로, 사진에서 추출한 feature를 Dense layer를 거쳐서 mean, log_var를 추출한다. 어차피 loss function을 거치면서 최적화될 것이다.
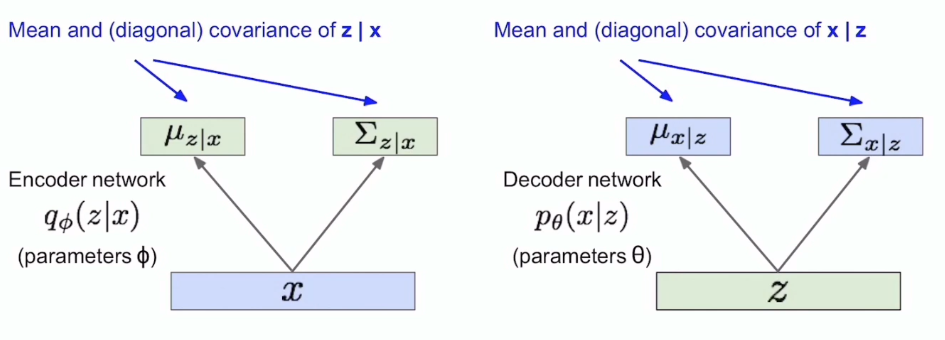
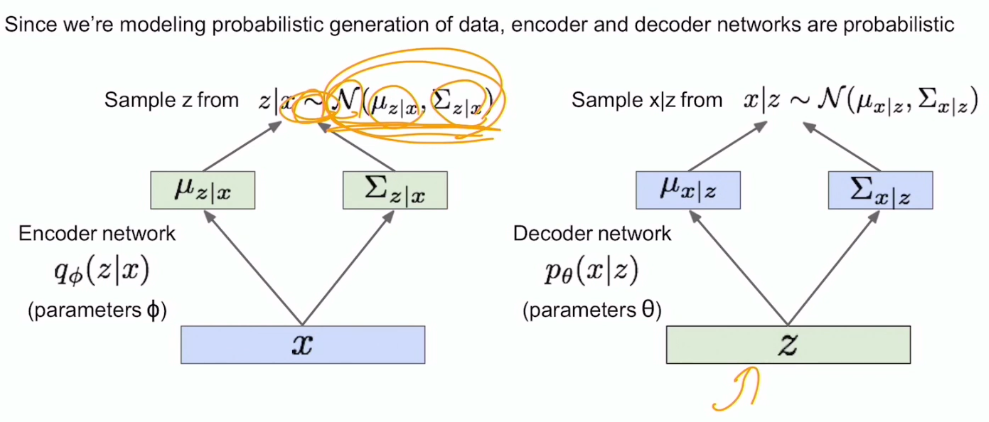
z는 가우시안 분포라고 가정을 했으므로,
Encoder 는 x를 받아서, z를 표현하는 μ, σ를 뽑아낸다.
Decoder는 z를 알 때, z분포로부터 sampling 한 임의의 벡터 z를 거쳐 μ, σ를 뽑아내는 역할을 한다.

def sampling(args):
# Reparameterization trick for back-propagation
z_mean, z_log_var = args
epsilon = K.random_normal(shape=(K.shape(z_mean)[0], latent_dim),
mean=0., stddev=1)
return z_mean + K.exp(z_log_var) * epsilon
# lambda 수식과 같은 임의의 함수를 layer 형태로 변환시켜주는 함수다.
z = layers.Lambda(sampling)([z_mean, z_log_var])여기서 이어주는 작업이 바로 z분포를 통해 z 벡터를 sampling 하는 일이다.
z는 가우시안 분포라고 가정을 했기 때문에, Encoder 통해 알고 있는 μ, σ 를 통해서 z를 위에 epsilon을 적용하여 하나 sampling 하고, sampling한 z벡터를 Decoder에 다시 통과시켜서 x를 만들어내는 작업 (새로운 output을 만들어내는 작업)을 한다.
sampling 작업에 noise를 부여함으로써 z벡터를 여러가지를 뽑고,p(x|z)를 거치면서 기존 x data와는 다른 분포를 가지는 x data가 나온다.
Decoder
# Decoder
decoder_input = layers.Input(K.int_shape(z)[1:])
x = layers.Dense(np.prod(shape_before_flattening[1:]),
activation='relu')(decoder_input)
x = layers.Reshape(shape_before_flattening[1:])(x)
x = layers.Conv2DTranspose(32, 3, padding='same', activation='relu',
strides=(2, 2))(x)
x = layers.Conv2D(1, 3, padding='same', activation='sigmoid')(x)
decoder = Model(decoder_input, x)
z_decoded = decoder(z)Loss Function
이제 실제로 우리가 예측한 pdf가 얼마나 잘 들어맞는지를 확인할 것이다.

logp(x)는 x라는 data의 실제 분포를 의미하는데, logp(x) 는 가능도함수이니 이를 max로 해야 확률이 높아져 좋은 것이다. 이를 max하는 경우는 q(z|x)를 거쳐 z를 거쳐 p(x|z)를 올 때의 평균값일 때 max이고 MLE이다.
우리는 z를 무한 sampling 하지 못하니, 베이지안 룰을 써서 다음과같이 설명할 수 있다.
여기서 맨 밑에 Dkl 부분은 실제로 두 모델이 얼마나 근접해있느냐에 수치를 나타낸 것이다. 0에 가까우면 근접, 숫자가 커질수록 두 모델은 서로 다른 분포를 가진다는 것을 의미한다. (Dkl은 0이상이다.)
Expectation 첫번째 항은 Decoder가 p(x|z)를 주는데, p(x|z)는 Feature z일 때 x일 likelihood 함수를 나타내기 때문에, p(x|z)가 클수록 "p(x)와 같은 값을 지닌다.", "parameter set인 θ가 잘 나타내는 것", "Decoder NN 가 잘 동작을 한다는 것", "Feature를 잘 포함하는 좋은 x를 뽑아내고 있다", "Reconstruction input data"을 의미한다.
두 번째 항은 "Encoder의 pdf와 z의 pdf의 유사도"를 나타낸 척도이다.
p(x)의 MLE를 위해서, 두 번째 항은 0에 근접, Encoder의 pdf = z의 pdf 유사해야만 MLE값은 최대가 될 수 있다.
Encoder NN의 pdf가 z의 pdf와 유사하다면, 이는 오차가 줄어들기 때문에 처음 input한 x와 output x의 오차가 줄어든다.
세 번째 항은 p(z|x)는 우리가 알 수 없기 때문에 항상 0이상이다.

따라서 ELBO 지점만 우리가 신경써서 무조건 높여주면 x라는 data의 model을 예측할 확률이 높아질 수가 있다.
ELBo 지점만 maximize하는 쪽으로 code를 작성하면 된다.
Loss Function Code

파이같이 생긴건 p(xij|zi)를 1부터 j까지 다 곱하라는 의미.
위는 사진 (사진은 베르누이, 0아니면 1이라는 분포를 띈다)일 때 해당된다.
log_var을 해주는 이유는 loss function에서 optimization을 할 경우, 발산하는 경우가 있기 때문에 ln을 씌워준다.
class CustomVariationalLayer(layers.Layer):
def vae_loss(self, x, z_decoded):
x = K.flatten(x)
z_decoded = K.flatten(z_decoded)
# 여기에서 - 가 곱해져 있다.
cross_entropy_loss = metrics.binary_crossentropy(x, z_decoded)
# kl_loss = 0.5 * K.mean(K.square(z_mean) + K.exp(z_log_var) - z_log_var - 1, axis=-1)
kl_loss = -5e-4 * K.mean(1 + z_log_var -
K.square(z_mean) - K.exp(z_log_var), axis=-1)
return K.mean(cross_entropy_loss + kl_loss)
def call(self, inputs):
x = inputs[0]
z_decoded = inputs[1]
loss = self.vae_loss(x, z_decoded)
self.add_loss(loss, inputs=inputs)
return x
y = CustomVariationalLayer()([input_layer, z_decoded])
vae = Model(input_layer, y)
vae.compile(optimizer='adam', loss=None)
vae.summary()
vae.fit(x=x_train, y=None, shuffle=True, epochs=30,
batch_size=100, validation_data=(x_test, None), verbose=1)
우리의 목표는 가능도함수인 p(x|z)를 p(x)로 최대한 근사시켜야한다. 그래야지 x와 근사한 x|z를 만들 수 있다.
또한 p(x)를 최대로, MLE가 최대를 목표로 한다. 이는 가능도함수가 max가 되는 지점이 input x 와 output x 와 같을 확률인 p(x)가 최대인 지점이므로, 우리가 원하는 data의 parameter를 알 수가 있는 지점이다.
VAE의 장단점
VAE는 GAN에 비해 학습이 안정적인 편이라고 합니다. 손실함수에서 확인할 수 있듯 reconstruction error과 같이 평가 기준이 명확하기 때문입니다. 아울러 데이터뿐 아니라 데이터에 내재한 잠재변수 z도 함께 학습할 수 있다는 장점이 있습니다(feature learning). 하지만 출력이 선명하지 않고 평균값 형태로 표시되는 문제, reparameterization trick이 모든 경우에 적용되지 않는 문제 등이 단점으로 꼽힌다고 합니다.
'AI' 카테고리의 다른 글
| 자연어처리 : Tagging Work (0) | 2020.03.23 |
|---|---|
| Math : Concave Function vs Convex Function (0) | 2020.03.19 |
| DL : VAE Reference (0) | 2020.03.18 |
| DL : Entropy, Cross Entropy (0) | 2020.03.18 |
| 자연어처리 : 절차적 단계가 뭘까? (0) | 2020.03.15 |




댓글