Introduction
앞서서 우리는 Model을 아는 경우, Dynamic Planning 을 통해서 True Value Function을 예측한다고 배웠다. 이 때 우리는 full-width backup, 즉, 모든 state들을 업데이트 할 수 있다. 왜냐하면 우리는 이미 model을 알고 있기 때문이다.
하지만 강화학습은 Model 을 모르는 경우이기 때문에 sample backup을 진행한다. 따라서 모든 state들을 고려하지 않고, 그 중에서 sampling을 통해서 한 길만 선택해서 가보는 것이다. 이처럼 sample backup을 하는 것은 Monte Carlo Method 와 TD Method 방법 두 가지가 있다.
그래서 실제로 알파고에도 쓰였던, 모든 step을 training 하는 Monte Carlo Method 에 대해 포스팅 할 것이다.
cf ) 실제로 알파고는 ‘Policy Function’과 ‘Value Function’이라 불리는 2개의 신경망으로 구성되었는데,
Policy Function이 다음 번 돌을 놓을 여러 경우의 수를 제시하면,
Value Function은 그중 가장 적합한 한 가지 예측치를 제시하는 역할을 한다.
이 과정에서 모든 경우의 수를 다 계산하는 것은 불가능하므로, 표본을 추출하여 승률을 어림잡는 몬테카를로 방법을 적용한 것이다.
Monte-Carlo Method
Monte Carlo Approximation

사실 Monte Carlo Approximation 는 원주율 문제를 구하는 예시가 제일 적절한 것 같아서 가져왔다.
원주율 문제를 구하는 문제는 여럿있지만, MC 방법은 우리가 원하는 값을 반복을 통해 근사시키는 개념이다.
위키피디아에 나온 정의는 다음과 같다.
MC 방법은 수학적인 결과를 얻기 위해 반복적으로 random sampling을 통해서 함수의 값을 확률적으로 계산하는 것이다. 이는 대수의 법칙에 의해 일부 random sampling의 예상값으로 설명되는 전체는 변수의 sample 평균을 취함으로써 근사치를 구할 수 있다.
하지만 통계학적인 관점에서 보면 다음과 같다.
MC 방법은 random sampling을 진행하고 모아서 우리가 관측한 System의 상태 분포를 알아내자는 접근이다.
위의 그림을 한 번 보자. 위의 그림 상태 분포는 원 안의 점을 찍을 확률 pi, 원 밖에 점을 찍을 확률 1-pi 두 가지 상태와 비율을 나타낸다.

주의할 점
Monte Carlo Approximation을 할 때 주의할 점은 random sampling이다. random sampling을 통해 함수의 값을 확률적으로 계산하기 때문에, 만약 random sampling이 bias가 생긴다면, 제대로된 함수를 찾지 못할 것이다.
Monte Carlo Method 목적
강화학습에서 Value Function을 학습하는 첫 번째 방법은 Monte-Carlo Method 라고 한다.
우리는 여기서 용어정리를 하고 갈 필요가 있다. (뒤에 가면서 굉장히 용어가 헷갈린다... 조심하자)
Agent는 S_1에서 시작해서 sampling한 state를 골라가며 S_T(Terminal State) 까지 간다.
Return : 이 때 받은 reward 들을 저장해두고 시간 순서대로 discounting 한 후 모두 더한 것이다.
Value Function : return들의 평균, 기댓값이다.

Dynamic Planning 의 경우는 iteration을 하면 모든 state에 대한 값이 다 나오기 때문에, state 값들을 정리해서 update하면 되지만,
Monte Carlo Method는 Model을 모르기 때문에 모든 state에 대한 function을 모른다.
따라서 한 episode를 마치고 얻은 각 state들의 return들의 평균값으로 value function을 근사하고 이를 반복해서 True value function을 얻자는 것이 핵심이다.
즉, 실제로 얻어진 n개의 return들의 평균으로 이 기댓값을 근사하는 것이다.
Monte Carlo Method Architecture



우선 N(s)는 total episode 동안 state s를 방문한 횟수, G(i)는 episode i번째에서 state s의 return 값이다.
이 식을 하나의 state 에 대해서만 생각하고 n개의 episode 를 했을 때,
V_n+1은 이 식을 S_T 의 state 에 대해서만 생각해보면, n개의 episode를 한 n개의 return 값을 통해 얻은 Value Function이다.
G_n 은 가장 최근에 얻은 return이고, 아래와 같이 점화식으로 표현 가능하다. (여기서 state의 index는 하나로 고정한 상태라 생략했다.)
우리는 state s에 대한 Value Function을 구해야한다. 하지만 model을 모르는 강화학습이기에 우리는 여러 episode를 겪으면서 state s에 대한 return 값들이 쌓인다. 이들을 평균을 내면 처음에는 분명 값이 다르지만, 어느정도 episode가 쌓인다면 이는 True Value Function에 근사할 것이다. 이게 포인트다!!


이 식은 새로운 return 값을 받았을 때, Value Function이 어떻게 update하는지를 점화식을 통해 알려준다.
따라서 return을 모두 모으고 한 번에 평균을 내는 것이 아니라 새로운 return 값이 올 때마다 update 해서 incremental 적으로 표현이 가능하다.
 |
 |
 |
마치 우리가 딥러닝할 때 Gradient 방법으로 학습할 때와 비슷하다. 알파가 learning rate 같은 역할을 한다.
여기서 1/n을 step size라고 표현하며, 이를 α라고 한다.
cf ) G_n 을 쓴 이유
이렇게 점화식으로 pseudo value function을 update 할 수 있기 때문이다.
이렇게 특정 state에 대해 episode n개의 return값으로 action-value function을 학습한 후에, policy는 각 state에서 최대의 action-value 값, max Q(s,a)을 갖는 action을 선택하게 된다.
여기서 Bellman Equation과 다른 점은 임의의 값을 대입해서 구한다.
cf) policy function을 쓰지 않고 Q(s,a)를 쓰는 이유

여기서 state value function V(s)를 안쓰는 이유는, 각 state에서 최적의 action을 고르는 policy를 계산할 때, 위의 그림에서 맨 아래의 수식을 써야하는데 이 식에는 transition probabilty (model) 이 필요하기 때문이다.
따라서 Monte Carlo Method 에서는 max point를 가져오기 때문에, policy function은 return의 평균값인 Q function 이 max인 부분만 따르면 되기 때문에 그림에서 밑줄 친 Transition과 Reward를 몰라도 가능하다는 것이다.
First-visit MC or Every visit MC
하나의 episode를 마치면 episode 동안 진행해왔던 state들 마다 return값이 존재하게 된다.
이 때, 중복 방문에 대한 return값을 처리하는 방식에 따라 first-visit MC와 every-visit MC로 나누어지는데,
- first-visit MC는 state에 첫 번째 방문했을 때의 return값만 취하고 두 번째 이후는 고려하지 않는다.
- every-visit MC는 이와 반대로 방문할 때마다 바뀐 return값으로 계산하는 것이다.
두 방법 모두 true value func.으로 수렴하지만 지금껏 다룬 내용은 모두 first-visit MC를 채택하여 다루었다.
결국 에피소드가 반복되면 무의미해진다. 그래서 그냥 First 많이쓰니까 이걸쓰자
Monte-Carlo Control
DP에서 Policy Iteration은 policy evaluation과 (greedy)policy improvement로 나누어진다. 여기서 policy evaluation에 MC를 이용하면 Monte-Carlo policy Iteration이 된다.
ㆍPolicy Iteration = ( policy evaluation + policy improvement )
ㆍMonte-Carlo policy Iteration = ( MC policy evaluation + policy improvement )
하지만 MC policy Iteration은 다음과 같은 문제점들이 존재하는데, 이를 해결한 것이 Monte-Carlo Control입니다.
1) Value function의 model-based
2) Local optimum
3) Inefficiency of policy evaluation
MC control은 위 문제점의 solution들을 어떻게 algorithm에 반영하였는지 살펴보겠습니다.
1) The attribute of value func. : model-based --> Q-function
MC로 policy evaluation을 하는 부분에서 value function을 이용한다. MC를 이용하는 것은 model-free의 속성을 이용하기 위해 도입했지만 value function을 사용하게 되면 policy를 improve할 때, model을 알아야만 한다.
따라서, value function 대신에 action-value function(q-function)을 이용하면 이를 해결할 수 있다.
value-function을 이용할 경우, agent가 episode마다 얻은 reward들로 state의 return값을 계산하고 이를 평균을 취해 state마다 value func.들을 계산해놓습니다. 이 과정이 MC policy evaluation이고 이를 통해 true value func.을 근사하여 얻을 수 있다. 하지만 improve과정에서 policy를 update할 때 아래의 식을 이용하는데, reward와 state transition prob.를 알아야 한다. Policy Iteration의 policy improvement 부분에서는 q.func.을 이용해서 policy를 update 했다. 이때, model이 쓰이기 때문에 q-func의 식대로 model 필요한 건 맞다.


action-value func.을 이용할 경우, return이 아닌 agent가 episode마다 random하게 움직이며 얻은 reward들 그리고 state transition prob.를 통해서 action-value func.을 계산할 수 있다. 이렇게 되면 policy를 improve할 때, model을 굳이 알지 못해도 이미 전 과정에서 q-func.을 이용함으로써 model의 정보가 다 담겨있습니다. 따라서 improve할 때는 이를 선택만 해주면 되는 문제이므로 model을 몰라도 improve 할 수 있다. 정리하자면 model-free하다는 개념은 policy를 improve할 때의 관점이고, q-func.자체는 model을 알아야지만 구할 수 있는 것은 맞다. 다만 trial and error의 과정 속에서 모든 정보가 q-func.에 담겨있으므로 policy improvement의 과정에서는 model-free 다.
2) Local optimum --> ε-greedy policy Improvement
Dynamic Programming에서 Policy를 improve하는 방법으로써 greedy policy improvement를 소개했다. 하지만 이 방법은 현 상황에서 제일 좋은 것만 찾는 매우 근시안적인 방법이라 local optimum에 빠지는 경우가 생긴다. 경사로의 공을 아래로 옮기는 일을 agent가 수행한다고 했을 때, 어떤 t시점에서의 slope가 t-1시점에서의 slope보다 계속 작아지는 쪽으로 옮기는 action을 취하면 된다. 하지만, 중간에 움푹 패인 골짜기를 만나게 된다면 더 이상 진행을 못하게 되고, 이 것이 local optimum에 빠진 현상이다.
우린 local에 빠지지 않도록 하는 작업을 가능하게 하는 것이 ε-greedy policy improvement 다. ε의 확률만큼 exploration을 하고, 1-ε의 확률만큼 empirical mean, 즉, 지금까지 observe한 것 중의 최적을 택하는 방법이다. exploration은 현재의 optimal 이외의 다른 무언가를 찾기 위해 random하게 action을 선택하는 것을 의미한다.
마치 Bayesian Optimization에서 Exploration, Exploitation과 똑같은 개념이다.
3) Inefficiency of policy evaluation --> one evaluation
DP에서 Policy Iteration의 과정을 optimal policy라는 전제와 함께 q-func.을 이용하여 단 한 번만 evaluation하는, Value Iteration이 있었다.
마찬가지로 MC control에서도 MC policy iteration에서의 evaluation을 단 한번만 진행하게 된다.
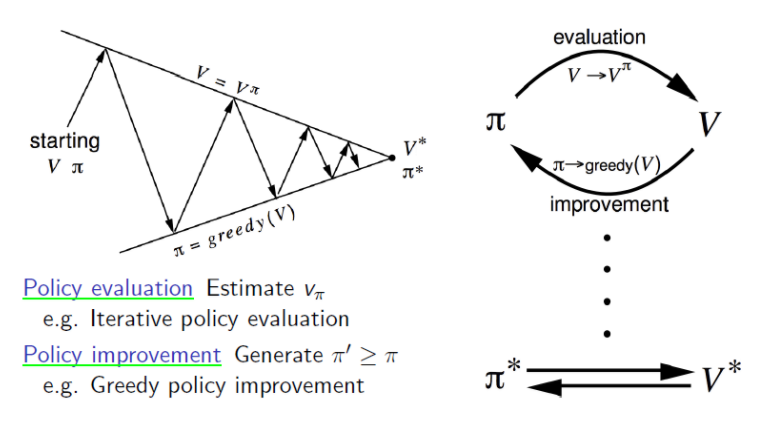
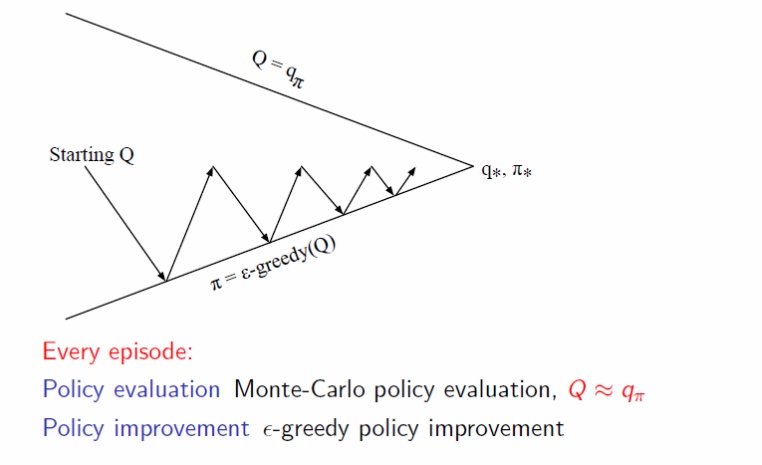
<Fig 4. Policy Iteration vs Monte-Carlo Control>
'AI' 카테고리의 다른 글
| RL : RL 용어정리 (0) | 2020.09.08 |
|---|---|
| RL : TD Method (0) | 2020.09.06 |
| RL : Empirical Learning [Model 모를 때] (0) | 2020.09.06 |
| RL : Dynaimc Planning [Model 알고있을 때] (0) | 2020.09.06 |
| RL : Value Function & Model (0) | 2020.09.06 |



댓글