앞서서 우리는 Dynamic Programming이 무엇인지에 대해 알고 있다.
2020/09/06 - [AI/RL] - RL : Dynamic Programming
RL : Dynamic Programming
출처 : velog.io/@cyranocoding/%EB%8F%99%EC%A0%81-%EA%B3%84%ED%9A%8D%EB%B2%95Dynamic-Programming%EA%B3%BC-%ED%83%90%EC%9A%95%EB%B2%95Greedy-Algorithm-3yjyoohia5 동적 계획법(Dynamic Programming)과 탐..
mambo-coding-note.tistory.com
next-state-value func.으로 present-state-value func.을 구하는 것을 Back-up이라고 합니다. backup을 진행하는 step에 따라 one-step backup (Monte Carlo) 과 multi-step backup (TD Method) 이 있고, 구하는 state의 종류에 따라 Full-width backup과 sample backup이 있습니다. DP는 value func.을 구할 때 바로 다음 step의 state value func.을 이용하기에 one-step backup이고, 현재 s에서 가능한 모든 s'들의 value func.을 구하기 때문에 Full-width backup입니다. (full-width는 모든 state들을 알 수 있기 때문에 가능하다.) 그러면 실제 grid-world에서 예제를 살펴보겠습니다.
Dynamic Planning : Model을 알고 있을 때

MDP의 요소중 transition function(T)와 reward function(R)을 ”model”이라고도 하는데, 이 model이 어떤 형태인지 알려져 있으면 planning이라는 방법을 사용하고, 알려져 있지 않으면 reinforcement learning을 사용한다.
Planning에서는 Dynamic Programming 이라는 기법을 사용해서 최적의 policy를 찾을 수 있다.
Dynamic Programming에 대한 자세한 설명을 아래 링크를 타고 보면 된다.
2020/09/06 - [mambo's coding note] - RL : Dynamic Programming
RL : Dynamic Programming
출처 : velog.io/@cyranocoding/%EB%8F%99%EC%A0%81-%EA%B3%84%ED%9A%8D%EB%B2%95Dynamic-Programming%EA%B3%BC-%ED%83%90%EC%9A%95%EB%B2%95Greedy-Algorithm-3yjyoohia5 동적 계획법(Dynamic Programming)과 탐..
mambo-coding-note.tistory.com
Dynamic Programming은 전체 큰 문제를 한 번에 푸는 것이 아니라, Step By Step으로 문제를 해결하는 방법이다.
소문제를 하나씩 풀다보면 언젠가는 결론에 도달한다는 것이다. 이러한 방법이 가능하려면 Model을 알아야 한다.
즉, Reward Function과 Transition Probabilty Function 두 가지 함수를 알아야 Step By Step이 가능해지기 때문이다.
Bellman Equation
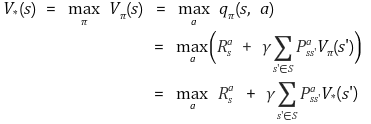

Bellman Equation 은 State-Value Function + Action-Value Function들의 관계로 현재 state/action , 다음 state/action 과의 관계식이다.
우리가 강화학습을 할 때는 초기화된 initial value(0 혹은 random number)를 여러 과정을 반복하며 얻은 정보들로 update하여 참 값을 얻도록 design되어 있다.
그리고 이렇게 반복적으로 얻은 값이 가장 클 때, 우리는 이를 Bellman Optimality Equation이라고 부른다.
cf) 여기서 P라는 변수가 나오는데, 현재(t) state s에서 다음(t+1) state s'으로 전이될 확률을 말한다.
Dynamic Planning 목적
state들은 MDP로 정의된다. 그리고 각 state를 통해서 value func.들이 존재합니다. True value func.이라 함은, 현재 따르는 policy가 옳냐 틀리냐를 판단하기 위해서 value func.을 사용하는데, 처음 구한 state의 value func.은 진짜 value func.이 아니다. 어쨌든 처음은 Random 하게 선택하기 때문에 error가 높기 때문이다.
몇 번이고 이 state 저 state를 반복적으로 이동하면서 value func.을 계속해서 update를 시켜 최종적으로 중요한지 안한지를 판단할 수 있는 "진짜" value func.을 찾는 것이다.
하지만 이 true value를 처음부터 구하기가 매우 어려우니 아래와 같이 iteration을 반복하며 점점 true value에 다가가자는 게 DP의 아이디어다.

MDP를 찾기 위한 Dynamic Programming에서 Bellman Equation을 만족하는 최적의 해답을 얻는 2가지 방법이 있다.
1. Policy iteration
- 정의
Policy iteration은 두 가지 단계로 나뉘는데, 먼저 policy evaluation은 현재 사용중인 policy의 value function을 계산한다. 반복적인 업데이트로 수렴한 value function은 최적은 아니며, 사용된 policy의 가치를 표현한다.
Policy iteration 에서는 얻어진 value-function을 기반으로 새로운 policy를 계산한다. 이 두 단계를 반복하면 최적의 policy를 구할 수 있다.
- Policy Evaluation

하나의 Iteration에서는 우리가 알고 있는 model을 이용해서 전체 state의 value func.을 모두 구한다. 이렇게 되면 무한히 반복되면서 데이터가 쌓이고 전체 state의 "진짜" 정보를 알게 되고 확실히 가야할 state도 알 수 있게 된다. 이렇게 policy 에 대한 true value func.을 구하기 위해 Iteration을 반복하는 것을 Policy Evaluation이라고 합니다.
- Policy Improvement

Policy Improvement 란 iteration을 반복하며 true value func.을 찾았으면 이 policy를 action을 취하면서 policy를 따르는 것이 좋은지 안 좋은지를 판단하고 Policy를 update 하는 단계다. policy를 improve하는 방법이 정해져 있는 것은 아니다. policy evaluation에서 state-value func.을 이용하여 모든 state들에 대해 value값을 구해놓았다면, 이제는 policy에 따른 action을 취해야한다. 이를 통해서 우리는 현재의 policy보다 더 나은 policy를 따르게 되고 점점 optimal policy에 가까워 질 것이다.
현재의 action은 random policy에 따라 random한 action을 취하는데, 우리는 Greedy policy improvement를 한다고 하면, 방법에 따라 현재 state에서 갈 수 있는 state 중 가장 높은 곳으로 이동하는 action을 취해야한다.
이러한 action을 정량화하여 선택하는 기준을 만드는 것이 위의 식인 q-func.(action-value func.)이다.
policy evaluation는 state의 value func.을 iterative하게 계산, 모든 state들에 대한 true value를 도출하는 과정이라면, policy improvement에서는 "도출된 true 라고 가정한 state value" 들을 토대로 현재의 policy를 action-value func.을 이용하여 더 좋은 action을 선택하는 policy로 만드는 과정이다.
2. Value iteration

Value iteration은 evaluation과정에서 이동 가능한 state s'들에 대해 모든 value func.들을 더하여 도출했지만, improvement step을 빼고 그냥 greedy 하게 max 값을 가지자 라는 것이 아이디어다. 그래서 우리는 action을 취할 확률을 곱해서 선택하는 것이 아니라, max값을 취하는 아래의 optimal value func.식을 사용합니다.
이렇게 한 슬라이드에 설명하기엔 다소 많은 내용인데, 자세한 설명은 아래의 자료들을 참고하면 좋다.
Bellman Equation: https://en.wikipedia.org/wiki/Bellman_equation
Value Iteration, Policy Iteration: http://people.eecs.berkeley.edu/~pabbeel/cs287-fa12/slides/mdps-exact-methods.pdf.
Wikipedia, the free encyclopedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search From today's featured article The Tweed Courthouse (officially the Old New York County Courthouse) is a historic courthouse building in Civic Center, Manhattan, New York City. Listed o
en.wikipedia.org
결론
- Dynamic Planning은 우리가 machine learning에서 다루는 learning이 아니라 planning이다.
- Policy iteration, Value iteration 던 True Value Function을 구하려고 하는 것인데 접근하는 계산법이 다른 것이다.
- 우리가 찾고자 하는 것은 각 state들의 true value func., Vπ(s) 이다.
- Dynamic Planning은 계산 복잡도가 state의 크기 3제곱에 비례하기 때문에 grid world보다 차원의 크기도 크고 state가 무수히 많은 실제 문제에 적용하기에는 많은 한계가 있다. 이를 보완한 것이, env.의 model을 몰라도 trial and error를 시행해보며 env.과 상호작용을 통해 알아가는, 강화학습이다.
다음 포스팅에서는 Reinforcement Learning에 적용되는 Monte Carlo Method, TD Method 방법에 대해서 포스팅할 예정이다.
'AI' 카테고리의 다른 글
| RL : Monte Carlo Method (0) | 2020.09.06 |
|---|---|
| RL : Empirical Learning [Model 모를 때] (0) | 2020.09.06 |
| RL : Value Function & Model (0) | 2020.09.06 |
| RL : Reinforcement Learning Element (0) | 2020.09.06 |
| RL : Dynamic Programming (0) | 2020.09.06 |




댓글