이전 포스팅에서는 강화학습의 간단한 개념들을 압축해서 설명해놓았다.
지금 포스팅에서는 강화학습에서 중요한 Element들에 대해서 자세하게 정의와 관계들을 정리할 것이다.
Markov Decision Process
위에서 MDP에 대한 내용이 굉장히 많이 나온다. 애초에 강화학습은 MDP의 구성요소를 차용한 것이다.
MDP 정의
우선 Markov Decision Process라고 하는것은 어떤 Agent의 의사결정 과정을 확률적인 모델 혹은 결정된 모델을 이용하여 모델링하는데 사용된다.
마르코프 결정 과정(MDP, Markov Decision Process)는 의사결정 과정을 모델링하는 수학적인 틀을 제공한다.
이 때 의사결정의 결과는 의사결정자의 결정에도 좌우되지만, 어느 정도 임의적으로 주어진다. 마르코프 결정 과정은 이산 시간 확률 제어 과정(discrete time stochastic control process)이다. 마르코프 결정 과정은 동적 계획법과 강화 학습 등의 방법으로 푸는 넓은 범위의 최적화 문제에 유용한 도구로 활용되며, 로봇 공학, 제어 자동화, 경제학, 제조업 등의 영역에서 폭넓게 사용되고 있다.


MDP는 5가지 요소로 구성되있는데, 이는 각각 state, action, reward function, transition function, 그리고 discount factor라고 한다.
State
state는 Agent의 상태를 나타내며, MDP의 첫 번째 요소인 S는 에이전트의 모든 state들의 집합을 나타낸다.
예를 들어 미로를 탈출하는 로봇의 경우, (x,y) 좌표로 나타낸 로봇의 위치가 state가 된다.
표기법으로는 s_0는 시작하는 상태, s는 현재 상태, s’은 다음 상태, 그리고 s_t는 t라는 시간에서의 상태를 나타낸다. 이 부분은 외워야 할 것 같다.
Action
action은 Agent가 취할 수 있는 행동이며 A는 에이전트의 모든 action의 집합이다.
이 로봇 의 경우 상하좌우 4개의 방향으로 1칸 이동하는 행동이 있다고 볼 수 있다. Agent는 본인의 action을 통해 현재상태 s를 그 다음 상태 s’으로 바꾸게 된다.
앞서 말한 state와 이 action은 s=(1,1), a=moveUp처럼 discrete 할 수 도 있고, 연속적인 실수값을 가질 수 도 있다.
Reward
R은 Agent에게 주어지는 보상을 구하는 함수다. 이 함수는 보통 Agent의 현재상태(s), 선택한 행동(a), 행동에 의해 바뀐 새로운 상태(s’) 3가지에 의해 결정된다.
예를 들어, 로봇 Agent가 상하좌우로 움직이면 배터리가 소모되기 때문에 -1의 보상을 줘서 움직임을 줄이라는 신호를 줄 수 도 있고, 보석을 얻거나 미로를 탈출하는데는 양수의 보상을 주어서 이런 행동을 더 많이 하라는 신호를 줄 수 있다.
여기서 중요한 것은, 이 Agent는 애초에 본인이 낭떠러지를 피해 미로를 탈출해야 된다는 목표가 있다는 점을 전혀 모른다는 점이다. 마치 애완견을 훈련시키듯, 안좋은 행동에는 낮은 (음수의) 보상을, 좋은 행동에는 높은 보상을 주며 보상을 통해 우리가 원하는 행동을 유도하는 것이다.
Transition
다음으로 T는 현재 상태(s)와 선택한 행동(a)이 주어졌을 때, 다음 상태(s’)를 결정하는 함수다.
같은 s, a가 주어졌을때 항상 같은 s’이 나오는 transition function은 ”deterministic”하다고 표현하고, 같은 s, a가 주어져도 s’에 대한 어떤 확률분포를 통해 결정되는 경우는 ”stochastic”하다고 표현한다. deterministic 방법은 매번 같은 결과가 나오고, Stochastic 경우는 확률분포에 의해 확률적으로 갈림길에 서서 여러가지 결과가 나온다고 볼 수 있다.
예를 들어, 그림과 같이 로봇 에이전트가 (1,0)위치에서 위로 한칸 움직였다고 할 때,
매번 (1,1)로 움직이는 것을 deterministic transition이라고 하고,
80% 확률로 (1,1)로 이동하고, 10% 확률로 (0,0)이나 (2,0)으로 이동하는 경우는 stochastic transition이라고 표현한다.
Discount Factor
마지막으로 discount factor라고 하는것은 0과 1사이의 값으로, Agent가 미래에 얻어지는 Reward을 얼마나 가치있다고 판단하는지를 정한다.
예를 들어, 미로에서 에이전트가 보석을 얻었을때 보상이 1이라고 하면, 에이전트가 한 스텝 나중에 보석을 얻는 것을 1보다 작은 (gamma*1)의 보상이라고 판단하는 것이다.
조금 더 쉬운 예로, 어린아이가 눈앞의 과자를 먹는 것과 한 시간 뒤에 먹는 것의 가치를 어떻게 생각할지 생각해보자.
이처럼 Markov Decision Process에 필요한 5가지 구성요소로 우리는 Value Function과 Policy & Return을 표현한다.
Markov Property : Memory Less

그럼 이렇게 말할 수 있다. 과거의 모든 상태들이 미래에 상태에 영향을 끼친다고 한다면, 우리는 과거의 상태들을 모두 기억하고 있어야 하는것인가??
MDP에서 한 단계 미래의 상태(s’)을 결정 하는데에는 오직 현재의 정보, s만 있으면 된다.
과거에 지나온 모든 상태와 행동들을 알 필요가 없고, 이는 현재의 상태 하나로 문제 해결이 가능하다.
이를 memory-less하다고 표현하며, MDP의 이런 성질을 Markov Property라고 한다.
지금까지는 강화학습에서 의사결정단계에 차용하는 MDP에 대해서 포스팅하였다.
그래서 이 MDP를 실제로 어떤 방식에 의해서 응용하고 적용하는지에 대해서 포스팅하려한다.
Policy & Return
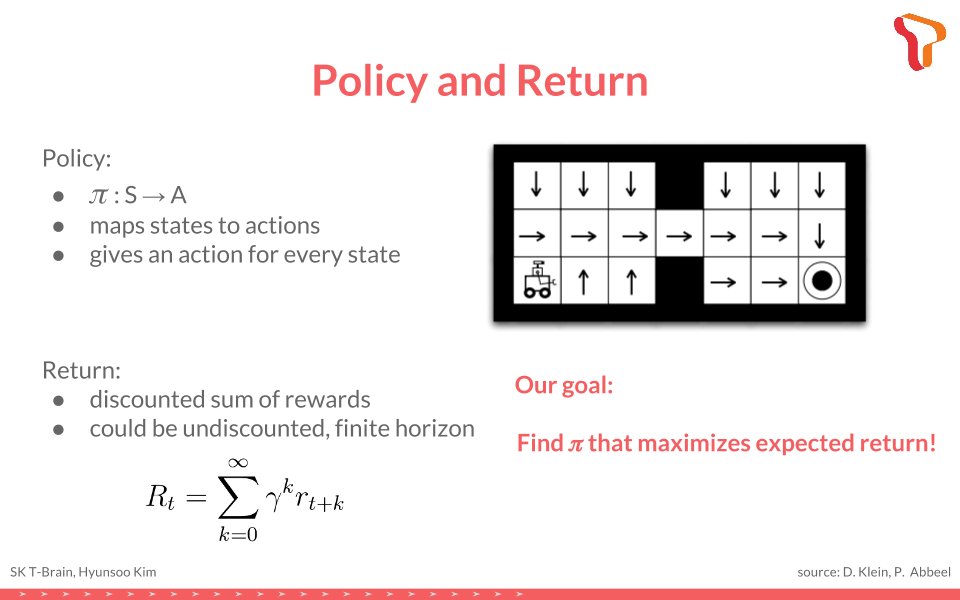
이렇게 MDP로 모델된 의사결정 과정에서 우리가 찾고 싶은건 최적의 의사결정이다. “각 상태마다 이 행동을 선택해야 제일 좋다"라고 알려주는 것을 policy(정책)라고 하고, 어떤 policy의 가치를 잴때 return이라는 것을 사용힌다.
로봇의 경우에 정책은 이렇게 각 위치에서 어떤 방향으로 이동해야하는지 알려준다.

Policy가 얼마나 좋은지 판단할때 쓰이는 기준으로 return을 쓰는데, 이는 여러가지 형태가 있다.
Policy 는 특정 상태에서 Agent의 Action과 Environment 의 State간의 관계를 도식화한 개념이다.
Action이 취하는 과정이 확률적으로 접근할 수 도 있고 (Stochastic) 정형화된 규칙 (Deterministic) 에 의해서도 결정될 수 있다.
Return은 Agent가 현재부터 얻은 reward의 총 합이 될수도 있고, 여기에 쓴 수식은 discounted Return이라고 하는데, 이렇게 각각의 reward를 언제 얻었냐에 따라 discount factor를 곱해서 더할 수 도 있다.
cf) Return을 나타내는 함수를 보면 K가 0일 때는 감마가 1인 것을 알 수 있다. Dicounted Factor는 step을 많이해서 도착지점에 도달하면 그 return의 가치는 떨어지기 때문에, 어차피 다음 step에서 도착한다면 reward는 dicounted 되지않기 때문에, 다음 step의 경우는 discounted factor는 1로 하는 것을 알 수 있다.
무한대의 시간까지 (로봇 에이전트가 시간제한 없이 탈출할 때까지) 모든 reward를 더하면 infinite horizon, 어떤 정해진 시간 제한을 두면 finite horizon이라고 한다.
이렇게 정의된 MDP, 그리고 policy와 return을 가지고 우리가 찾고싶은 것은 최적의 policy, 즉 return을 최대화 시키는 policy다.
'AI' 카테고리의 다른 글
| RL : Dynaimc Planning [Model 알고있을 때] (0) | 2020.09.06 |
|---|---|
| RL : Value Function & Model (0) | 2020.09.06 |
| RL : Dynamic Programming (0) | 2020.09.06 |
| RL : Reinforcement Learning 기본 개념 (0) | 2020.08.30 |
| RL : Reinforcement Learning 사례 (0) | 2020.08.30 |




댓글